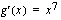 , joten ulkofunktio on
, joten ulkofunktio on 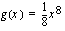 ja sisäfunktion
ja sisäfunktion 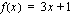 derivaatta on
derivaatta on 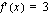 Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke
Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke 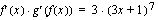 .
.
a ) Ulkofunktion derivaatta on 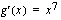 , joten ulkofunktio on
, joten ulkofunktio on 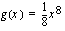 ja sisäfunktion
ja sisäfunktion 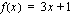 derivaatta on
derivaatta on 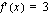 Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke
Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke 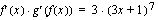 .
.
b ) Yhdistetty funktio on määritelty, kun 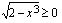 . Ratkaistaan määrittelyjoukko.
. Ratkaistaan määrittelyjoukko.
Huomaa, että kerrottaessa negatiivisella luvulla epäyhtälön merkki kääntyy. Yhdistetty funktio on määritelty, kun 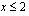 .
.
Ulkofunktion derivaatta on 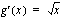 , joten ulkofunktio on
, joten ulkofunktio on 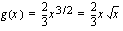 ja sisäfunktion
ja sisäfunktion 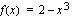 derivaatta on
derivaatta on 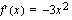 . Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke
. Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke 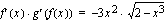 .
.
c ) Jaetaan summan integraali ensin paloihin.
Ensimmäisessä integraalissa ulkofunktion derivaatta on 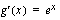 , joten ulkofunktio on
, joten ulkofunktio on 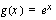 ja sisäfunktion
ja sisäfunktion 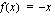 derivaatta on
derivaatta on 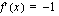 . Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke
. Integroitavaa funktiota täytyy hieman muokata, jotta integroitavaksi saadaan lauseke 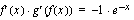 .
.
[Tehtävä 11.2][Vinkki tehtävään 11.2]