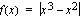Ratkaisu tehtävään 10.9

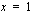a ) Tutkitaan funktion 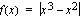derivoituvuus kohdassa .

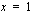Ollakseen derivoituva funktion täytyy olla jatkuva, joten tutkitaan ensin funktion jatkuvuus. Tämän tekemiseksi poistetaan funktion 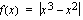itseisarvot. Tutkitaan, milloin itseisarvon sisällä oleva lauseke 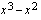on positiivinen muodostamalla funktion merkkikaavio, jota varten täytyy laskea lausekkeen 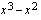nollakohdat tulon nollasääntöä avuksi käyttäen.

Tulon nollasäännön mukaan tulo on nolla, jos toinen tulon tekijöistä on nolla.

tai .

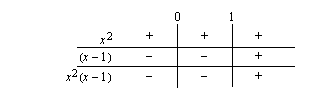
Funktio voidaan nyt kirjoittaa paloittain määriteltynä

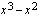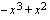ja ovat polynomeina jatkuvia ja derivoituvia 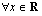. Funktion 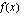jatkuvuus ja derivoitavuus kohdassa 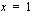on tarkasteltava erikseen.

Funktio on jatkuva kohdassa 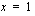, jos sen toispuoleiset raja-arvot

ovat yhtäsuuret.

Raja-arvot ovat samat, joten funktio 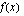on jatkuva kohdassa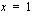

Funktion on derivoituva, jos funktion toispuoleiset derivaatat ovat yhtäsuuria kohdassa 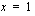. Lasketaan funktion 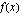derivaatta:

Seuraavien lausekkeiden tulee olla yhtäsuuria:

Funktion toispuoleiset derivaatat ovat erisuuret, joten funktio 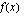ei ole derivoituva kohdassa .

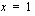b ) Osoitetaan, että funktiolla 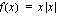on derivaatta kohdassa .

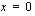Ollakseen derivoituva funktion täytyy olla jatkuva, joten tutkitaan ensin funktion jatkuvuus. Tämän tekemiseksi poistetaan funktion 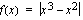itseisarvot. Kirjoitetaan funktio paloittain määriteltynä

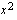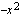ja ovat polynomeina jatkuvia ja derivoituvia 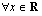. Funktion 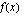jatkuvuus ja derivoitavuus kohdassa 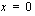on tarkasteltava erikseen.

Funktio on jatkuva kohdassa 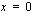, jos sen toispuoleiset raja-arvot

ovat yhtäsuuret.

Raja-arvot ovat samat, joten funktio 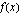on jatkuva kohdassa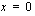

Funktion on derivoituva, jos funktion toispuoleiset derivaatat ovat yhtäsuuria kohdassa 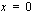. Lasketaan funktion 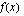derivaatta:

Seuraavien lausekkeiden tulee olla yhtäsuuria:

Funktion toispuoleiset derivaatat ovat yhtäsuuret, joten funktio 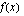on derivoituva kohdassa 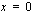ja derivaatan arvo on .

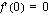[Tehtävä 10.9][Vinkki tehtävään 10.9]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]