Ratkaisu tehtävään 10.8

a ) Kyseisen tangenttisuoran suuntakulma saadaan suuntakulman ja kulmakertoimen välisen yhteyden avulla. Määritetään funktion

kuvaajalle kohtaan 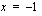piirretyn tangenttisuoran kulmakerroin.

Tangentin kulmakerroin saadaan laskemalla funktion derivaatan arvo kohdassa .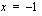

Lasketaan funktion derivaatta

Lasketaan tangentin kulmakerroin sijoittamalla 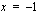derivaatan lausekkeeseen.

Funktion

kuvaajalle kohtaan 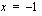piirretyn tangenttisuoran suuntakulma saadaan yhtälöstä . Suuntakulma saadaan laskimen avulla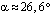

b ) Määritetään vakio 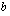siten, että funktiot 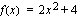ja 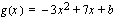omaavat leikkauspisteessään saman derivaatan arvon. Lasketaan kyseisen derivaatan arvo ja pohditaan mitä tulos tarkoittaa geometrisesti.

Ratkaistaan derivaattojen lausekkeet

ja

Ratkaistaan funktioiden kuvaajien leikkauspisteet ratkaisemalla yhtälö .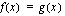

Siirretään kaikki termit yhtälön vasemmalle puolelle. Yhdistetään samanmuotoiset termit ja ratkaistaan kuvaajien leikkauspisteiden 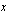-koordinaatit toisen asteen yhtälön ratkaisukaavan avulla.

Toisen asteen yhtälön ratkaisukaava

Kuvaajilla on kaksi leikkauspistettä, jos 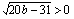, jolloin funktioiden derivaatat eivät voi saada samaa arvoa, sillä funktion 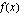kuvaaja on ylöspäin aukeava paraabeli ja funktion 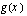kuvaaja on alaspäin aukeava paraabeli. Kuvaajilla on yksi leikkauspiste, jos 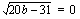, jolloin funktioiden kuvaajat sivuavat toisiaan kohdassa 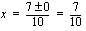. Vakion 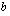arvo saadaan ratkaisemalla eo. yhtälö.

Derivaattojen arvot ovat nyt samat, mutta lasketaan varmuuden vuoksi molemmat erikseen.

ja

[Tehtävä 10.8][Vinkki tehtävään 10.8]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]