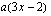 ja
ja 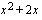 ovat polynomeina jatkuvia ja derivoituvia
ovat polynomeina jatkuvia ja derivoituvia 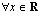 . Funktion
. Funktion 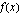 jatkuvuuden vuoksi on tarkastettava kohta
jatkuvuuden vuoksi on tarkastettava kohta 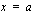 .
.
a ) 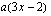 ja
ja 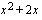 ovat polynomeina jatkuvia ja derivoituvia
ovat polynomeina jatkuvia ja derivoituvia 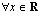 . Funktion
. Funktion 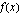 jatkuvuuden vuoksi on tarkastettava kohta
jatkuvuuden vuoksi on tarkastettava kohta 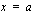 .
.
Funktio on jatkuva kohdassa 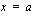 , jos sen toispuoleiset raja-arvot
, jos sen toispuoleiset raja-arvot
Vakio 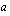 saadaan nyt määrätty yhtälöstä
saadaan nyt määrätty yhtälöstä 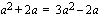 siirtämällä kaikki termit yhtälön vasemmalle puolelle, yhdistämällä samanmuotoiset termit ja ottamalla yhteiseksi tekijäksi
siirtämällä kaikki termit yhtälön vasemmalle puolelle, yhdistämällä samanmuotoiset termit ja ottamalla yhteiseksi tekijäksi 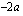 , jolloin voidaan käyttää tulon nollasääntöä.
, jolloin voidaan käyttää tulon nollasääntöä.
b ) Edellisen kohdan nojalla funktio 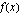 on jatkuva, jos
on jatkuva, jos 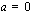 tai
tai 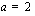 . Funktion derivoitavuus vaatii, että funktion toispuoleisten derivaattojen pitää olla yhtäsuuria kohdassa
. Funktion derivoitavuus vaatii, että funktion toispuoleisten derivaattojen pitää olla yhtäsuuria kohdassa 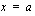 . Lasketaan funktion
. Lasketaan funktion 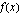 derivaatta:
derivaatta:
Ts. seuraavien lausekkeiden tulee olla yhtäsuuria:
[Tehtävä 10.10][Vinkki tehtävään 10.10]