Ratkaisu tehtävään 10.6
Suljetulla välillä 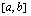 jatkuva funktio
jatkuva funktio 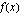 on aidosti kasvava, jos sen derivaatalle pätee (yksittäisiä pisteitä lukuunottamatta, joissa
on aidosti kasvava, jos sen derivaatalle pätee (yksittäisiä pisteitä lukuunottamatta, joissa 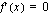 tai
tai 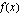 ei ole derivoituva), että
ei ole derivoituva), että 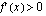 . Tämän tutkimiseksi funktio on derivoitava ja on muodostettava derivaatan merkkikaavio, jonka avulla funktion kasvavuus voidaan todeta. Derivaatan merkkikaaviota varten on laskettava derivaatan nollakohdat
. Tämän tutkimiseksi funktio on derivoitava ja on muodostettava derivaatan merkkikaavio, jonka avulla funktion kasvavuus voidaan todeta. Derivaatan merkkikaaviota varten on laskettava derivaatan nollakohdat
a ) Funktio 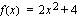 on kaikkialla jatkuva ja derivoituva ja sen derivaatta saadaan derivoimalla termeittäin.
on kaikkialla jatkuva ja derivoituva ja sen derivaatta saadaan derivoimalla termeittäin.
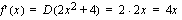
Lasketaan derivaatan nollakohdat ratkaisemalla yhtälö 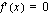 .
.
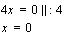
Ensimmäisen asteen yhtälön ratkaisu eli derivaatan nollakohta on 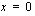 .
.
Muodostetaan derivaatan merkkikaavio. Derivaattafunktion kuvaaja on nouseva suora, joten se saa arvoja seuraavalla tavalla.
Funktio 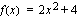 on aidosti kasvava, kun
on aidosti kasvava, kun 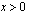
b ) Funktio 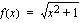 on kaikkialla jatkuva ja derivoituva. Yhdistetyn funktion derivoimissäännön avulla (sisäfunktio on
on kaikkialla jatkuva ja derivoituva. Yhdistetyn funktion derivoimissäännön avulla (sisäfunktio on 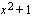 ja ulkofunktio
ja ulkofunktio 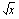 ).
).
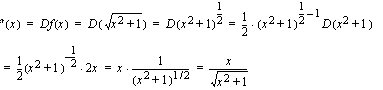
Derivaattafunktion 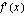 nimittäjä
nimittäjä 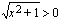 , joten
, joten 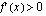 kun
kun 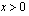 .
.
Funktio 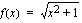 on aidosti kasvava, kun
on aidosti kasvava, kun 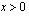
[Tehtävä 10.6][Vinkki tehtävään 10.6]
[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]
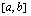 jatkuva funktio
jatkuva funktio 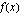 on aidosti kasvava, jos sen derivaatalle pätee (yksittäisiä pisteitä lukuunottamatta, joissa
on aidosti kasvava, jos sen derivaatalle pätee (yksittäisiä pisteitä lukuunottamatta, joissa 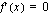 tai
tai 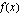 ei ole derivoituva), että
ei ole derivoituva), että 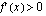 . Tämän tutkimiseksi funktio on derivoitava ja on muodostettava derivaatan merkkikaavio, jonka avulla funktion kasvavuus voidaan todeta. Derivaatan merkkikaaviota varten on laskettava derivaatan nollakohdat
. Tämän tutkimiseksi funktio on derivoitava ja on muodostettava derivaatan merkkikaavio, jonka avulla funktion kasvavuus voidaan todeta. Derivaatan merkkikaaviota varten on laskettava derivaatan nollakohdat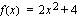 on kaikkialla jatkuva ja derivoituva ja sen derivaatta saadaan derivoimalla termeittäin.
on kaikkialla jatkuva ja derivoituva ja sen derivaatta saadaan derivoimalla termeittäin.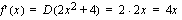
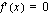 .
.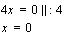
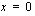 .
.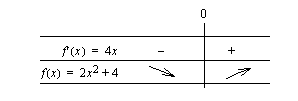
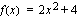 on aidosti kasvava, kun
on aidosti kasvava, kun 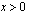
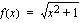 on kaikkialla jatkuva ja derivoituva. Yhdistetyn funktion derivoimissäännön avulla (sisäfunktio on
on kaikkialla jatkuva ja derivoituva. Yhdistetyn funktion derivoimissäännön avulla (sisäfunktio on 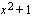 ja ulkofunktio
ja ulkofunktio 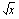 ).
).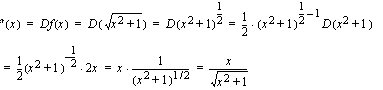
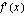 nimittäjä
nimittäjä 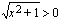 , joten
, joten 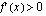 kun
kun 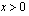 .
. 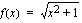 on aidosti kasvava, kun
on aidosti kasvava, kun