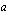arvot, joilla funktio
a ) Ratkaistaan ne vakion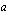
arvot, joilla funktio
Funktio on polynomina selvästi jatkuva ja derivoituva, kun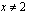 
.
Kohta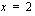 
vaatii tarkempia tarkasteluja. Kohdassa 
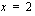on oltava voimassa jatkuvuusehto, jonka mukaan seuraavien lausekkeiden on oltava yhtäsuuria:
Saadaan yhtälö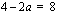 
. Ratkaistaan vakion 
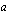arvo, jolla funktio 
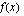on jatkuva kohdassa 
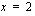ratkaisemalla saatu yhtälö.
Funktio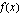 
on jatkuva vakion 
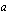arvolla 
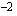. Funktio voidaan nyt kirjoittaa muodossa
b ) Määritetään vakio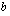 
siten, että funktio
Funktio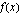 
on epäjatkuva nimittäjänsä nollakohdissa 
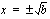, toisin sanoen funktio 
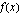on jatkuva määrittelyjoukossaan 
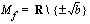. Määrätään vakio 
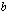siten, että se toteuttaa annetun ehdon.
Funktio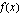 
on epäjatkuva kohdissa 
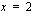ja 
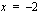, kun vakio 
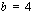, jolloin funktio on muotoa
[Tehtävä 9.11][Vinkki tehtävään 9.11]
ja 
.
