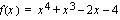on jatkuva ja derivoituva 
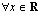. Valitaan kaksi muuttujan 
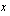arvoa ja katsotaan mitä niitä vastaavia arvoja funktio saa.
Funktio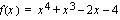
on jatkuva ja derivoituva
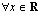. Valitaan kaksi muuttujan
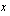arvoa ja katsotaan mitä niitä vastaavia arvoja funktio saa.
Bolzanon lauseen nojalla funktiolla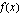 
on olemassa ainakin yksi nollakohta 
.
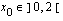Koska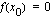 
on myös 
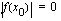. Toisaalta 
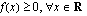ja edellä on todistettu, että 
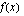saavuttaa arvon nolla edes yhdessä kohdassa 
, 
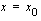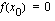joten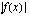 
:n pienin arvo on nolla.
[Tehtävä 9.12][Vinkki tehtävään 9.12]
