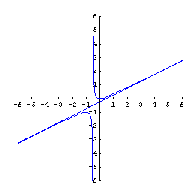Ratkaisu tehtävään 10.7
Rationaalifunktion 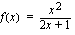 osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen -
osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen - 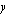 -akselin suuntainen suora - saadaan nimittäjän nollakohdasta
-akselin suuntainen suora - saadaan nimittäjän nollakohdasta 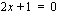 ja toinen - muotoa
ja toinen - muotoa 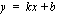 oleva suora - saadaan suorittamalla jakolasku
oleva suora - saadaan suorittamalla jakolasku 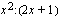 jakokulmassa ja jättämällä jäännöstermi huomiotta.
jakokulmassa ja jättämällä jäännöstermi huomiotta.
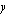 -akselin suuntainen suora:
-akselin suuntainen suora:
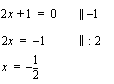
Muotoa 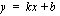 oleva suora:
oleva suora:
Funktion lauseke voidaan kirjoittaa muodossa:
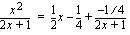
Kun 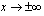 , niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa
, niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa 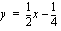 , mikä on funktion kuvaajan asymptootti.
, mikä on funktion kuvaajan asymptootti.
Funktiolla 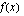 on asymptootit
on asymptootit 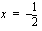 ja
ja 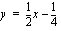 .
.
Funktion kuvaajan piirtämiseksi täytyy selvittää funktion vähenevyys/kasvavuus. Edellisen tehtävän 10.6.b) kohdassa on selvitetty funktion käyttäytyminen, joten käytetään tietoja hyväksi..
Funktio 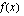 on aidosti kasvava, kun
on aidosti kasvava, kun 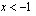 ja aidosti vähenevä, kun
ja aidosti vähenevä, kun 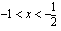 . Funktio
. Funktio 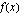 on aidosti vähenevä, kun
on aidosti vähenevä, kun 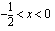 ja aidosti kasvava, kun
ja aidosti kasvava, kun 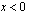 . Rationaalifunktion kuvaaja voidaan nyt piirtää asymptoottien ja funktion käyttäytymisestä selvitettyjen tietojen avulla.
. Rationaalifunktion kuvaaja voidaan nyt piirtää asymptoottien ja funktion käyttäytymisestä selvitettyjen tietojen avulla.
[Tehtävä 10.7][Vinkki tehtävään 10.7]
[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]
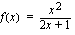 osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen -
osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen - 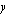 -akselin suuntainen suora - saadaan nimittäjän nollakohdasta
-akselin suuntainen suora - saadaan nimittäjän nollakohdasta 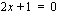 ja toinen - muotoa
ja toinen - muotoa 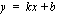 oleva suora - saadaan suorittamalla jakolasku
oleva suora - saadaan suorittamalla jakolasku 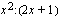 jakokulmassa ja jättämällä jäännöstermi huomiotta.
jakokulmassa ja jättämällä jäännöstermi huomiotta.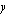 -akselin suuntainen suora:
-akselin suuntainen suora: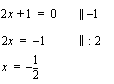
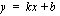 oleva suora:
oleva suora: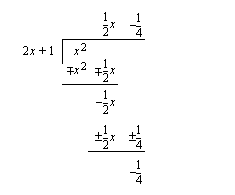
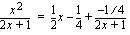
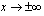 , niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa
, niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa 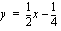 , mikä on funktion kuvaajan asymptootti.
, mikä on funktion kuvaajan asymptootti.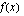 on asymptootit
on asymptootit 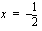 ja
ja 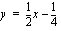 .
.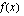 on aidosti kasvava, kun
on aidosti kasvava, kun 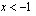 ja aidosti vähenevä, kun
ja aidosti vähenevä, kun 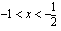 . Funktio
. Funktio 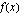 on aidosti vähenevä, kun
on aidosti vähenevä, kun 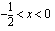 ja aidosti kasvava, kun
ja aidosti kasvava, kun 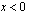 . Rationaalifunktion kuvaaja voidaan nyt piirtää asymptoottien ja funktion käyttäytymisestä selvitettyjen tietojen avulla.
. Rationaalifunktion kuvaaja voidaan nyt piirtää asymptoottien ja funktion käyttäytymisestä selvitettyjen tietojen avulla.