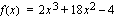 on polynomina jatkuva ja derivoituva. Lasketaan funktion derivaatta.
on polynomina jatkuva ja derivoituva. Lasketaan funktion derivaatta.
a ) Funktio 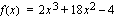 on polynomina jatkuva ja derivoituva. Lasketaan funktion derivaatta.
on polynomina jatkuva ja derivoituva. Lasketaan funktion derivaatta.
Lasketaan derivaatan nollakohdat 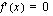 .
.
Yhtälö on vaillinainen toisen asteen yhtälö, josta puuttuu vakiotermi, joten se voidaan ratkaista tulon nollasääntöä käyttäen ottamalla ensin yhteiseksi tekijäksi 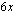 .
.
Tulon nollasäännön mukaan joko 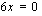 tai
tai 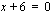 . Derivaatalla on siis nollakohdat
. Derivaatalla on siis nollakohdat 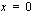 ja
ja 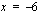 . Muodostetaan derivaatan merkkikaavio, jonka avulla voidaan päätellä funktion
. Muodostetaan derivaatan merkkikaavio, jonka avulla voidaan päätellä funktion  käyttäytyminen. Derivaatta on toisen asteen polynomi, jonka kuvaaja on ylöspäin aukeava paraabeli. Sen merkkikaavio saadaan siis helposti.
käyttäytyminen. Derivaatta on toisen asteen polynomi, jonka kuvaaja on ylöspäin aukeava paraabeli. Sen merkkikaavio saadaan siis helposti.
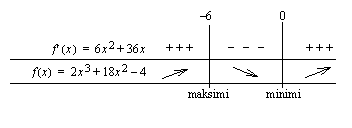
Funktiolla 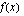 on lokaali maksimi kohdassa
on lokaali maksimi kohdassa 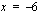 jolloin
jolloin 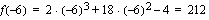 ja lokaali minimi kohdassa
ja lokaali minimi kohdassa 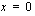 jolloin
jolloin 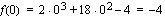 . Funktiolla on siis maksimipiste
. Funktiolla on siis maksimipiste 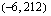 ja minimipiste
ja minimipiste 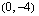 ja se on aidosti monotoninen, kun
ja se on aidosti monotoninen, kun 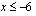 tai
tai 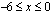 tai
tai 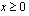 .
.
b ) Funktio 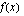 on määritelty, kun nimittäjä
on määritelty, kun nimittäjä 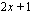 on nollasta eroava.
on nollasta eroava.
Nimittäjän nollakohta saadaan ratkaisemalla yhtälö 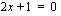 . Vähentämällä molemmilta puolilta 1 ja jakamalla muuttujan
. Vähentämällä molemmilta puolilta 1 ja jakamalla muuttujan 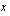 kerroin 2 pois saadaan nollakohdaksi
kerroin 2 pois saadaan nollakohdaksi
Funktio 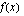 on siis jatkuva ja derivoituva, kun
on siis jatkuva ja derivoituva, kun 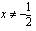 .
.
Funktion derivaatta 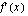 saadaan osamäärän derivoimissäännön avulla
saadaan osamäärän derivoimissäännön avulla
Lasketaan derivaatan nollakohdat. Murtofunktio on nolla, kun osoittaja on nolla. Derivaatan nollakohdat saadaan siis osoittajan 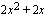 nollakohdista ratkaisemalla yhtälö
nollakohdista ratkaisemalla yhtälö 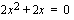 . Yhtälö on vaillinainen toisen asteen yhtälö, josta puuttuu vakiotermi, joten se voidaan ratkaista tulon nollasääntöä käyttäen ottamalla ensin yhteiseksi tekijäksi
. Yhtälö on vaillinainen toisen asteen yhtälö, josta puuttuu vakiotermi, joten se voidaan ratkaista tulon nollasääntöä käyttäen ottamalla ensin yhteiseksi tekijäksi 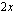 .
.
Tulon nollasäännön mukaan joko 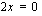 tai
tai 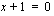 . Derivaatalla on siis nollakohdat
. Derivaatalla on siis nollakohdat 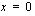 ja
ja 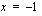 . Muodostetaan derivaatan merkkikaavio (huomioi myös nimittäjän nollakohta), jonka avulla voidaan päätellä funktion
. Muodostetaan derivaatan merkkikaavio (huomioi myös nimittäjän nollakohta), jonka avulla voidaan päätellä funktion 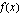 käyttäytyminen.
käyttäytyminen.
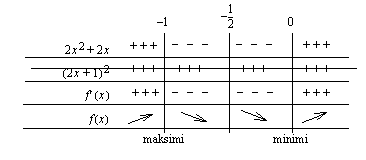
Funktiolla 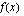 on lokaali maksimi kohdassa
on lokaali maksimi kohdassa 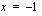 jolloin
jolloin
ja lokaali minimi kohdassa 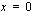 jolloin
jolloin
Funktiolla on siis maksimipiste 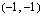 ja minimipiste
ja minimipiste 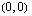 ja se on aidosti monotoninen, kun
ja se on aidosti monotoninen, kun 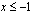 tai
tai 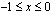 tai
tai 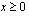 .
.
[Tehtävä 10.6][Vinkki tehtävään 10.6]