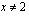.
Funktio on polynomina selvästi jatkuva ja derivoituva, kun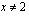
.
Kohta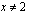 
vaatii tarkempia tarkasteluja. Kohdassa 
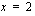on oltava voimassa jatkuvuusehto, jonka mukaan seuraavien lausekkeiden on oltava yhtäsuuria:
Lisäksi funktion derivoituvuudesta saadaan seuraava ehto, jonka mukaan funktion toispuoleisten derivaattojen pitää olla yhtäsuuria kohdassa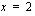 
. Lasketaan funktion 
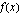derivaatta:
Ts. seuraavien lausekkeiden tulee olla yhtäsuuria:
Edellisten ehtojen yhtälöistä saadaan yhtälöpari (molempien ehtojen täytyy olla voimassa), jonka ratkaisemalla saadaan vakiot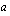 
ja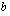 
määrättyä siten, että funktio on derivoituva kaikkialla, myös kohdassa 
.
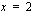Sijoittamalla alempi yhtälö ylempään saadaan yhtälö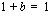 
josta edelleen 
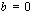. Sijoittamalla tämä ylempään yhtälöön saadaan 
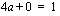, josta edelleen jakamalla molemmat puolet neljällä saadaan 
.
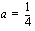Ehdot toteuttava (kaikkialla derivoituva) funktio on siis
[Tehtävä 10.5][Vinkki tehtävään 10.5]
.
