5.3.1. Kappaleen nopeus
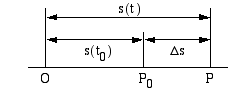 Tarkastellaan suoraviivaisessa liikkeessä olevan kappaleen kulkemaa matkaa
Tarkastellaan suoraviivaisessa liikkeessä olevan kappaleen kulkemaa matkaa 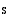 ajan
ajan 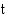 funktiona. Matka on mitattu pisteestä
funktiona. Matka on mitattu pisteestä 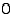 lähtien. Hetkellä
lähtien. Hetkellä 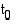 kappale on pisteessä
kappale on pisteessä 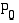 ja sen kulkema matka on
ja sen kulkema matka on 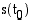 . Hetkellä
. Hetkellä 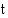 kappale on pisteessä
kappale on pisteessä 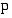 ja sen kulkema matka on
ja sen kulkema matka on 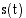 . Kappaleen
keskinopeus
. Kappaleen
keskinopeus 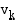 aikavälillä
aikavälillä 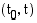 saadaan jakamalla kappaleen kulkema matka
saadaan jakamalla kappaleen kulkema matka 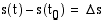 siihen käytetyllä ajalla
siihen käytetyllä ajalla 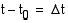 :
:
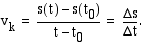
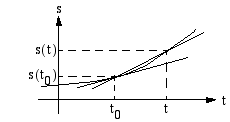 Oheiseen koordinaatistoon on piirretty tämän kappaleen kulkema matka
Oheiseen koordinaatistoon on piirretty tämän kappaleen kulkema matka 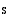 ajan
ajan 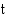 funktiona. Kappaleen keskinopeus
funktiona. Kappaleen keskinopeus 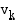 aikavälillä
aikavälillä 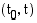 , joka on
, joka on
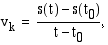
on geometrisesti tulkittuna matkafunktion kuvaajan pisteiden 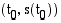 ja
ja 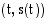 kautta kulkevan sekantin kulmakerroin.
kautta kulkevan sekantin kulmakerroin.
Kappaleen hetkellinen nopeus ajanhetkellä 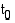 saadaan sen keskinopeuden raja-arvona, kun annetaan aikavälin
saadaan sen keskinopeuden raja-arvona, kun annetaan aikavälin 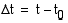 lähestyä nollaa, jolloin
lähestyä nollaa, jolloin 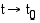 . Kappaleen
hetkellinen nopeus
. Kappaleen
hetkellinen nopeus 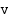 , kun
, kun 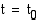 on siten
on siten
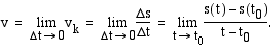
Kun 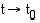 , matkafunktion kuvaajalle piirretty sekantti kiertyy pisteeseen
, matkafunktion kuvaajalle piirretty sekantti kiertyy pisteeseen 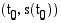 piirretyn tangentin (sivuajan) suuntaiseksi. Koska kappaleen keskinopeus aikavälillä
piirretyn tangentin (sivuajan) suuntaiseksi. Koska kappaleen keskinopeus aikavälillä 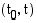 on tuon sekantin kulmakerroin, on keskinopeuden raja-arvo - kappaleen hetkellinen nopeus - pisteeseen
on tuon sekantin kulmakerroin, on keskinopeuden raja-arvo - kappaleen hetkellinen nopeus - pisteeseen 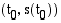 piirretyn tangentin kulmakerroin.
piirretyn tangentin kulmakerroin.
Esimerkki 5.8.
Kohtisuoraan ylöspäin heitetyn pallon korkeus 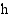 (m) ajan
(m) ajan 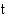 (s) funktiona on
(s) funktiona on
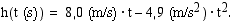
Laske pallon nopeus 1 (s) kuluttua heittohetkestä.
Ratkaisu:
Pallon hetkellinen nopeus 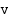 1 (s) kuluttua heitosta on edellä johdetun määritelmän nojalla
1 (s) kuluttua heitosta on edellä johdetun määritelmän nojalla
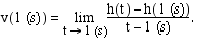
Sijoitetaan pallon korkeuden ilmoittava funktio lausekkeeseen ja lasketaan nopeuden antava raja-arvo. On helppo havaita, että korkeusfunktio on yksiköiden puolesta hyvin määritelty. Jätetään raja-arvon määrityksessä mittayksiköt selvyyden vuoksi pois.
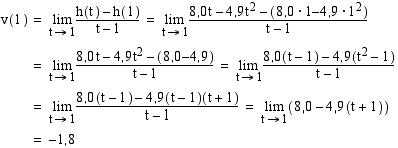
Raja-arvon ottaminen ei vaikuta mittayksiköihin. Koska pallon nopeus saatiin raja-arvona lausekkeelle 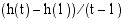 , jonka mittayksikkö on (m/s), on pallon nopeus
, jonka mittayksikkö on (m/s), on pallon nopeus 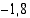 (m/s).
(m/s).
Vastaus: Pallon nopeus on 1 (s) kuluttua heittohetkestä 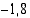 (m/s). Nopeuden negatiivisuus kertoo, että pallon suunta on tällöin alaspäin.
(m/s). Nopeuden negatiivisuus kertoo, että pallon suunta on tällöin alaspäin.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
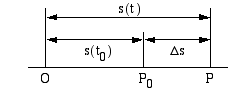 Tarkastellaan suoraviivaisessa liikkeessä olevan kappaleen kulkemaa matkaa
Tarkastellaan suoraviivaisessa liikkeessä olevan kappaleen kulkemaa matkaa 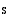 ajan
ajan 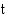 funktiona. Matka on mitattu pisteestä
funktiona. Matka on mitattu pisteestä 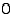 lähtien. Hetkellä
lähtien. Hetkellä 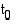 kappale on pisteessä
kappale on pisteessä 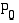 ja sen kulkema matka on
ja sen kulkema matka on 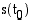 . Hetkellä
. Hetkellä 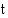 kappale on pisteessä
kappale on pisteessä 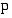 ja sen kulkema matka on
ja sen kulkema matka on 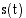 . Kappaleen
keskinopeus
. Kappaleen
keskinopeus 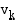 aikavälillä
aikavälillä 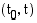 saadaan jakamalla kappaleen kulkema matka
saadaan jakamalla kappaleen kulkema matka 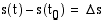 siihen käytetyllä ajalla
siihen käytetyllä ajalla 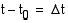 :
: 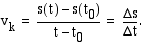
 Oheiseen koordinaatistoon on piirretty tämän kappaleen kulkema matka
Oheiseen koordinaatistoon on piirretty tämän kappaleen kulkema matka 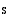 ajan
ajan 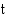 funktiona. Kappaleen keskinopeus
funktiona. Kappaleen keskinopeus 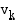 aikavälillä
aikavälillä 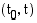 , joka on
, joka on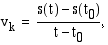
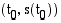 ja
ja 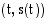 kautta kulkevan sekantin kulmakerroin.
kautta kulkevan sekantin kulmakerroin. 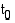 saadaan sen keskinopeuden raja-arvona, kun annetaan aikavälin
saadaan sen keskinopeuden raja-arvona, kun annetaan aikavälin 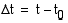 lähestyä nollaa, jolloin
lähestyä nollaa, jolloin 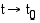 . Kappaleen
hetkellinen nopeus
. Kappaleen
hetkellinen nopeus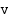 , kun
, kun 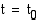 on siten
on siten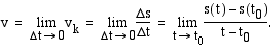
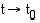 , matkafunktion kuvaajalle piirretty sekantti kiertyy pisteeseen
, matkafunktion kuvaajalle piirretty sekantti kiertyy pisteeseen 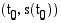 piirretyn tangentin (sivuajan) suuntaiseksi. Koska kappaleen keskinopeus aikavälillä
piirretyn tangentin (sivuajan) suuntaiseksi. Koska kappaleen keskinopeus aikavälillä 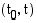 on tuon sekantin kulmakerroin, on keskinopeuden raja-arvo - kappaleen hetkellinen nopeus - pisteeseen
on tuon sekantin kulmakerroin, on keskinopeuden raja-arvo - kappaleen hetkellinen nopeus - pisteeseen 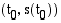 piirretyn tangentin kulmakerroin.
piirretyn tangentin kulmakerroin. 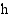 (m) ajan
(m) ajan 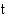 (s) funktiona on
(s) funktiona on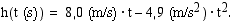
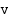 1 (s) kuluttua heitosta on edellä johdetun määritelmän nojalla
1 (s) kuluttua heitosta on edellä johdetun määritelmän nojalla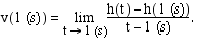
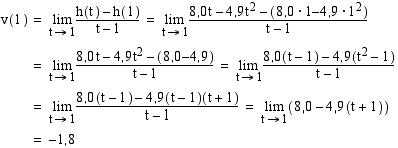
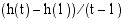 , jonka mittayksikkö on (m/s), on pallon nopeus
, jonka mittayksikkö on (m/s), on pallon nopeus 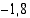 (m/s).
(m/s). 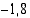 (m/s). Nopeuden negatiivisuus kertoo, että pallon suunta on tällöin alaspäin.
(m/s). Nopeuden negatiivisuus kertoo, että pallon suunta on tällöin alaspäin.