4.7.3. Trigonometriset funktiot
Trigonometristen funktioiden määritelmät
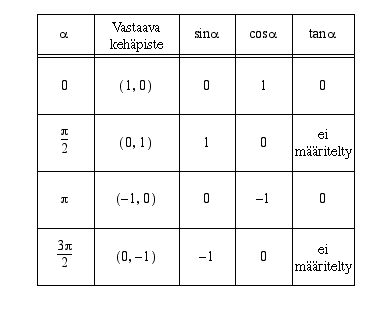
Jatkossa käytetään kulman yksikkönä pelkästään radiaania ja sen yksikkömerkintä (rad) jätetään pois. Määritellään trigonometriset funktiot uudelleen näille kulmille, joiden suuruus on annettu radiaaneina. Tällä tavoin saadaan trigonometrisista funktioista reaalimuuttujan funktioita. Olkoon yksikköympyrään piirrettyä kulmaa 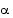 vastaava kehäpiste
vastaava kehäpiste 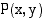 . Asetetaan uudet määritelmät niin, että terävien kulmien tapauksessa ne yhtyvät suorakulmaisen kolmion sivujen suhteisiin perustuviin määritelmiin.
. Asetetaan uudet määritelmät niin, että terävien kulmien tapauksessa ne yhtyvät suorakulmaisen kolmion sivujen suhteisiin perustuviin määritelmiin.
Seuraavassa esimerkissä on laskettu näiden määritelmien avulla joidenkin tavallisten kulmien trigonometristen funktioiden arvot.
Esimerkki 4.36.
Trigonometristen funktioiden tarkkoja arvoja eräille tavallisille kulmille löytyy taulukkokirjoista. Funktioiden likiarvot voidaan määrittää laskimella. Kun laskimella määritetään radiaaneina ilmaistun kulman sinin, kosinin tai tangentin arvoja, on laskin ensin asetettava radiaanitilaan. Sen tunnuksena on laskimen näytössä R-kirjain tai lyhenne RAD. Yleensä radiaanitilaan päästään DRG-näppäimellä, jota painellaan, kunnes ollaan halutussa tilassa. (DRG-näppäimen tilat vastaavat kolmea eri kulmanyksikköä. D-tilassa kulman yksikkö on aste (engl. degree), R-tilassa radiaani ja G-tilassa graadi. [
Graadi eli gooni (gon) on ns. uusaste, joka on suoran kulman sadasosa. Sitä käytetään mm. maanmittaustekniikassa.
]) Eräissä laskimissa eri kulmanyksikkötilat valitaan omasta valikosta.
Esimerkki 4.37.
Määrää likiarvot
(a) 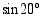
(b) 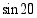
(c) 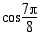
Vastaus: Likiarvot ovat (a) 0,342 (b) 0,913 (c) 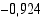
Trigonometristen funktioiden määrittely- ja arvojoukot
Trigonometristen funktioiden 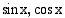 ja
ja 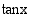 määrittely- ja arvojoukot voidaan päätellä niiden määritelmistä. Sini- ja kosinifunktiot on määritelty kaikilla reaaliarvoilla. Koska niiden arvo on yksikköympyrän kehäpisteen
määrittely- ja arvojoukot voidaan päätellä niiden määritelmistä. Sini- ja kosinifunktiot on määritelty kaikilla reaaliarvoilla. Koska niiden arvo on yksikköympyrän kehäpisteen 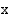 - tai
- tai 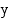 -koordinaatti, joka kuuluu aina välille
-koordinaatti, joka kuuluu aina välille 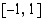 , on sini- ja kosinifunktiolle voimassa
, on sini- ja kosinifunktiolle voimassa
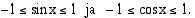
Tangenttifunktio
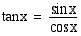
on määritelty ainoastaan, kun 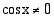 . Koska kosinifunktio
. Koska kosinifunktio 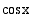 saa arvon nolla, kun
saa arvon nolla, kun
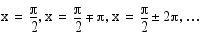
on tangenttifunktio 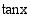 määritelty, kun
määritelty, kun 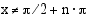 , missä
, missä 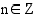 . Koska tangenttifinktio on sinin ja kosinin osamäärä, joka voi saada kaikki mahdolliset reaaliarvot, on tangenttifunktion arvojoukko reaalilukujen joukko. Seuraavassa taulukossa on yhteenveto trigonometristen funktioiden määrittely- ja arvojoukoista.
. Koska tangenttifinktio on sinin ja kosinin osamäärä, joka voi saada kaikki mahdolliset reaaliarvot, on tangenttifunktion arvojoukko reaalilukujen joukko. Seuraavassa taulukossa on yhteenveto trigonometristen funktioiden määrittely- ja arvojoukoista.
Kulman 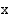 trigonometristen funktioiden merkit voidaan päätellä, kun tiedetään, mihin neljännekseen kulman loppukylki kuuluu. Seuraavista kuvioista ilmenee sinin, kosinin ja tangentin merkit eri neljänneksissä.
trigonometristen funktioiden merkit voidaan päätellä, kun tiedetään, mihin neljännekseen kulman loppukylki kuuluu. Seuraavista kuvioista ilmenee sinin, kosinin ja tangentin merkit eri neljänneksissä.
Trigonometristen funktioiden jaksollisuus
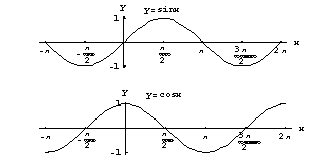 Trigonometristen funktioiden tärkein ominaisuus on niiden jaksollisuus. Se ilmenee parhaiten, kun tarkastellaan funktioiden kuvaajia. Oheisessa kuvassa ovat sini- ja kosinifunktion kuvaajat. Kummankin funktion kuvaajat toistuvat samanlaisina
Trigonometristen funktioiden tärkein ominaisuus on niiden jaksollisuus. Se ilmenee parhaiten, kun tarkastellaan funktioiden kuvaajia. Oheisessa kuvassa ovat sini- ja kosinifunktion kuvaajat. Kummankin funktion kuvaajat toistuvat samanlaisina 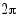 :n välein. Sanotaan, että funktioiden perusjakso on
:n välein. Sanotaan, että funktioiden perusjakso on 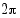 . Sinifunktion arvohan on kulmaa vastaavan kehäpisteen
. Sinifunktion arvohan on kulmaa vastaavan kehäpisteen 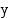 -koordinaatti ja kosinin
-koordinaatti ja kosinin 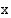 -koordinaatti. Kun loppukylki on kiertänyt täyden kierroksen eli kulman
-koordinaatti. Kun loppukylki on kiertänyt täyden kierroksen eli kulman 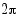 verran, kehäpiste palaa takaisin alkupisteeseen ja aloittaa saman kierroksen alusta. Siten sekä sini- että kosinifunktion arvot toistuvat samanlaisina
verran, kehäpiste palaa takaisin alkupisteeseen ja aloittaa saman kierroksen alusta. Siten sekä sini- että kosinifunktion arvot toistuvat samanlaisina 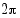 :n välein:
:n välein:
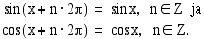
Tangentti on myös jaksollinen funktio. Sen perusjakso on  :
:
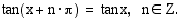
Oheisesta tangenttifunktion kuvaajasta ilmenee, kuinka se saa saman arvon aina  :n välein.
:n välein.
Jaksollisuutensa ansiosta trigonometriset funktiot toimivat matemaattisena mallina erilaisille jaksollisille ilmiöille. Tällaisia ovat esim. heilurin liike tasapainoasemansa molemmin puolin, vaihtovirta ja -jännite, vuorovesi, Maan pyörähdysliike akselinsa ympäri ja kiertoliike Auringon ympäri sekä taloustieteessä suhdannekierto ym. jaksolliset vaihtelut. Uusilla trigonometrian sovellusaloilla ei siis ole paljonkaan tekemistä kolmioiden tai kulmien kanssa.
Esimerkki 4.38.
Vuoroveden takia satamassa veden korkeus 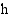 (m) noudattaa funktiota
(m) noudattaa funktiota
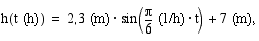
missä 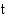 on keskiyöstä kulunut aika tunteina. Kuinka korkealla sataman vesi on (a) klo 8.00 (b) klo 14.00?
on keskiyöstä kulunut aika tunteina. Kuinka korkealla sataman vesi on (a) klo 8.00 (b) klo 14.00?
Ratkaisu:
(a) Kun 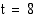 (h), korkeus on
(h), korkeus on
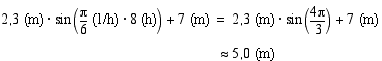
(b) Kun 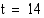 (h), korkeus on
(h), korkeus on
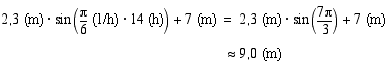
Vastaus: (a) 5,0 (m) (b) 9,0 (m)
Trigonometriset yhtälöt
Tarkastellaan trigonometrisia yhtälöitä, jotka ovat muotoa
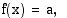
missä 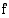 on jokin trigonometrinen funktio ja
on jokin trigonometrinen funktio ja 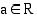 . Koska sini, kosini ja tangentti saavat jaksollisina funktioina jokaisen arvonsa äärettömän monta kertaa, trigonometrisilla yhtälöillä on yleensä äärettömän monta ratkaisua.
. Koska sini, kosini ja tangentti saavat jaksollisina funktioina jokaisen arvonsa äärettömän monta kertaa, trigonometrisilla yhtälöillä on yleensä äärettömän monta ratkaisua.
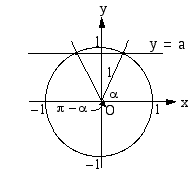 Yhtälöllä
Yhtälöllä
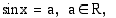
on ratkaisuja ainoastaan, kun 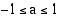 . Tällöin niitä on äärettömän monta. Jos yhtälöllä
. Tällöin niitä on äärettömän monta. Jos yhtälöllä 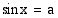 on ratkaisu
on ratkaisu 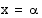 , niin myös
, niin myös  on ratkaisu. Koska sinifunktion perusjakso on
on ratkaisu. Koska sinifunktion perusjakso on 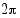 , yhtälön
, yhtälön 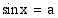 kaikki ratkaisut ovat
kaikki ratkaisut ovat
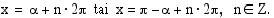
Esimerkki 4.41.
Ratkaise yhtälö
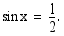
Ratkaisu:
Koska 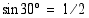 , yhtälön eräs ratkaisu on
, yhtälön eräs ratkaisu on 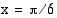 . Tällöin muut ratkaisut ovat
. Tällöin muut ratkaisut ovat
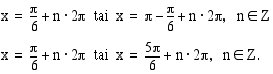
Vastaus: 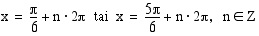
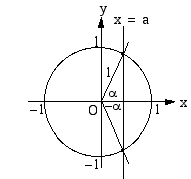 Yhtälöllä
Yhtälöllä
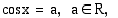
on myös ratkaisuja ainoastaan, kun 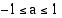 . Jos
. Jos 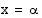 on yhtälön
on yhtälön 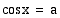 ratkaisu,
ratkaisu, 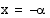 on myös sen ratkaisu. Koska kosinifunktion perusjakso on
on myös sen ratkaisu. Koska kosinifunktion perusjakso on 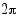 , yhtälön kaikki ratkaisut ovat
, yhtälön kaikki ratkaisut ovat
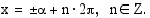
Esimerkki 4.42.
Ratkaise yhtälö 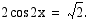
Ratkaisu:
Muutetaan yhtälö ensin muotoon
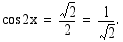
Koska
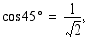
yhtälön eräs ratkaisu on 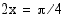 . Yhtälön kaikki ratkaisut ovat
. Yhtälön kaikki ratkaisut ovat
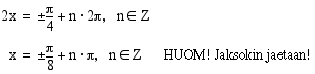
Vastaus: 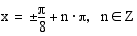
Yhtälöllä
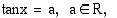
on aina äärettömän monta ratkaisua. Tangentin kuvaajasta nähdään, että funktio saa jokaisen arvonsa aina  :n välein. Jos yhtälön
:n välein. Jos yhtälön 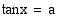 eräs ratkaisu on
eräs ratkaisu on 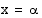 , sen kaikki ratkaisut ovat
, sen kaikki ratkaisut ovat
Esimerkki 4.43.
Ratkaise yhtälö 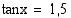 .
.
Ratkaisu:
Laskimella saadaan yhdeksi ratkaisuksi 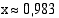 . Yhtälön kaikki ratkaisut ovat
. Yhtälön kaikki ratkaisut ovat
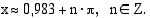
Vastaus: 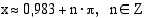
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
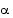 vastaava kehäpiste
vastaava kehäpiste 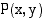 . Asetetaan uudet määritelmät niin, että terävien kulmien tapauksessa ne yhtyvät suorakulmaisen kolmion sivujen suhteisiin perustuviin määritelmiin.
. Asetetaan uudet määritelmät niin, että terävien kulmien tapauksessa ne yhtyvät suorakulmaisen kolmion sivujen suhteisiin perustuviin määritelmiin. 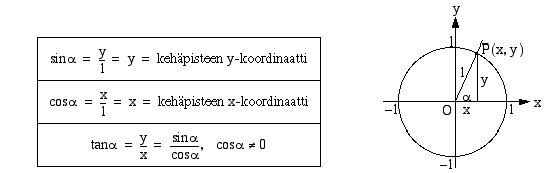
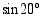
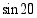
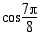
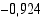
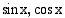 ja
ja 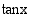 määrittely- ja arvojoukot voidaan päätellä niiden määritelmistä. Sini- ja kosinifunktiot on määritelty kaikilla reaaliarvoilla. Koska niiden arvo on yksikköympyrän kehäpisteen
määrittely- ja arvojoukot voidaan päätellä niiden määritelmistä. Sini- ja kosinifunktiot on määritelty kaikilla reaaliarvoilla. Koska niiden arvo on yksikköympyrän kehäpisteen 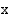 - tai
- tai 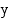 -koordinaatti, joka kuuluu aina välille
-koordinaatti, joka kuuluu aina välille 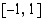 , on sini- ja kosinifunktiolle voimassa
, on sini- ja kosinifunktiolle voimassa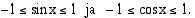
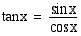
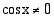 . Koska kosinifunktio
. Koska kosinifunktio 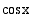 saa arvon nolla, kun
saa arvon nolla, kun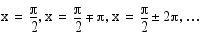
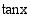 määritelty, kun
määritelty, kun 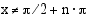 , missä
, missä 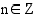 . Koska tangenttifinktio on sinin ja kosinin osamäärä, joka voi saada kaikki mahdolliset reaaliarvot, on tangenttifunktion arvojoukko reaalilukujen joukko. Seuraavassa taulukossa on yhteenveto trigonometristen funktioiden määrittely- ja arvojoukoista.
. Koska tangenttifinktio on sinin ja kosinin osamäärä, joka voi saada kaikki mahdolliset reaaliarvot, on tangenttifunktion arvojoukko reaalilukujen joukko. Seuraavassa taulukossa on yhteenveto trigonometristen funktioiden määrittely- ja arvojoukoista. 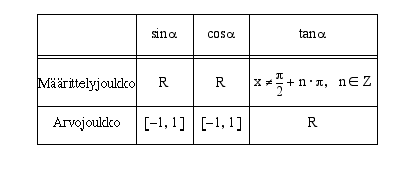
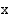 trigonometristen funktioiden merkit voidaan päätellä, kun tiedetään, mihin neljännekseen kulman loppukylki kuuluu. Seuraavista kuvioista ilmenee sinin, kosinin ja tangentin merkit eri neljänneksissä.
trigonometristen funktioiden merkit voidaan päätellä, kun tiedetään, mihin neljännekseen kulman loppukylki kuuluu. Seuraavista kuvioista ilmenee sinin, kosinin ja tangentin merkit eri neljänneksissä. 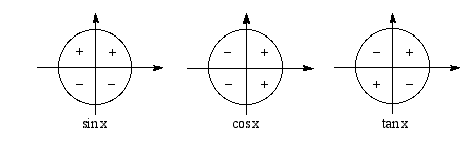
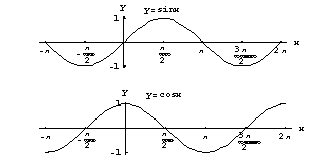 Trigonometristen funktioiden tärkein ominaisuus on niiden jaksollisuus. Se ilmenee parhaiten, kun tarkastellaan funktioiden kuvaajia. Oheisessa kuvassa ovat sini- ja kosinifunktion kuvaajat. Kummankin funktion kuvaajat toistuvat samanlaisina
Trigonometristen funktioiden tärkein ominaisuus on niiden jaksollisuus. Se ilmenee parhaiten, kun tarkastellaan funktioiden kuvaajia. Oheisessa kuvassa ovat sini- ja kosinifunktion kuvaajat. Kummankin funktion kuvaajat toistuvat samanlaisina 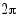 :n välein. Sanotaan, että funktioiden perusjakso on
:n välein. Sanotaan, että funktioiden perusjakso on 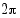 . Sinifunktion
. Sinifunktion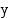 -koordinaatti ja kosinin
-koordinaatti ja kosinin 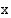 -koordinaatti. Kun loppukylki on kiertänyt täyden kierroksen eli kulman
-koordinaatti. Kun loppukylki on kiertänyt täyden kierroksen eli kulman 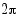 verran, kehäpiste palaa takaisin alkupisteeseen ja aloittaa saman kierroksen alusta. Siten sekä sini- että kosinifunktion
verran, kehäpiste palaa takaisin alkupisteeseen ja aloittaa saman kierroksen alusta. Siten sekä sini- että kosinifunktion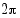 :n välein:
:n välein: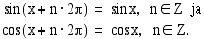
 :
: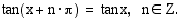
 :n välein.
:n välein. 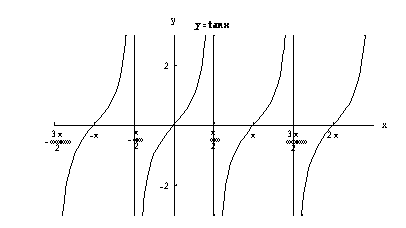
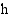 (m) noudattaa funktiota
(m) noudattaa funktiota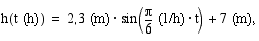
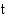 on keskiyöstä kulunut aika tunteina. Kuinka korkealla sataman vesi on (a) klo 8.00 (b) klo 14.00?
on keskiyöstä kulunut aika tunteina. Kuinka korkealla sataman vesi on (a) klo 8.00 (b) klo 14.00?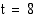 (h), korkeus on
(h), korkeus on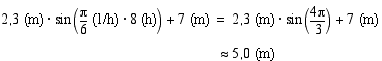
 (h), korkeus on
(h), korkeus on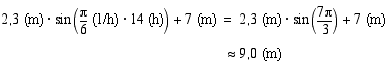
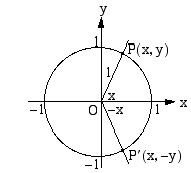 Sini- ja kosinifunktiolla on useita symmetriaan perustuvia ominaisuuksia. Tarkastellaan ensin kulmia
Sini- ja kosinifunktiolla on useita symmetriaan perustuvia ominaisuuksia. Tarkastellaan ensin kulmia 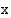 ja
ja 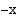 , joiden loppukyljet sijaitsevat symmetrisesti
, joiden loppukyljet sijaitsevat symmetrisesti 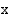 -akseliin nähden. Kulmia vastaavien kehäpisteiden
-akseliin nähden. Kulmia vastaavien kehäpisteiden 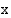 -koordinaatit ovat samat, joten kulmien kosinit ovat yhtäsuuret:
-koordinaatit ovat samat, joten kulmien kosinit ovat yhtäsuuret: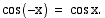
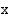 ja
ja 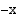 vastaavien kehäpisteiden
vastaavien kehäpisteiden 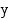 -koordinaatit ovat toistensa vastalukuja, on voimassa
-koordinaatit ovat toistensa vastalukuja, on voimassa 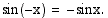
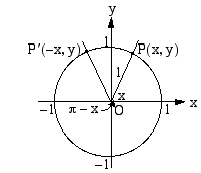 Tarkastellaan sitten kulmia
Tarkastellaan sitten kulmia 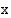 ja
ja 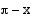 , joita vastaavat kehäpisteet sijaitsevat symmetrisesti
, joita vastaavat kehäpisteet sijaitsevat symmetrisesti 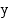 -akselin suhteen. Tällöin niiden
-akselin suhteen. Tällöin niiden 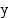 -koordinaatit ovat samat eli kulmien sinit ovat yhtäsuuret:
-koordinaatit ovat samat eli kulmien sinit ovat yhtäsuuret: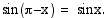
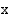 ja
ja 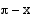 vastaavien kehäpisteiden
vastaavien kehäpisteiden 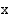 -koordinaatit ovat toistensa vastalukuja, jolloin on voimassa:
-koordinaatit ovat toistensa vastalukuja, jolloin on voimassa: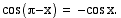
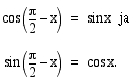
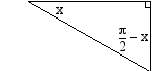
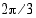 trigonometristen funktioiden arvot.
trigonometristen funktioiden arvot. 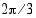 on
on 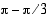 , joten sen trigonometristen funktioiden arvot saadaan kulman
, joten sen trigonometristen funktioiden arvot saadaan kulman 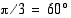 trigonometristen funktioiden ja symmetriaominaisuuksien avulla.
trigonometristen funktioiden ja symmetriaominaisuuksien avulla.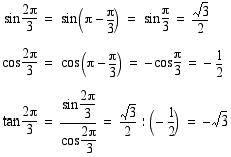
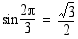 ,
, 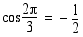 ja
ja 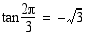 .
.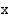 vastaava kehäpiste
vastaava kehäpiste 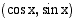 on origokeskisellä yksikköympyrällä, joten sen koordinaatit toteuttavat tämän ympyrän yhtälön
on origokeskisellä yksikköympyrällä, joten sen koordinaatit toteuttavat tämän ympyrän yhtälön 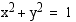 . Tämän nojalla kulman
. Tämän nojalla kulman 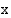 sinin ja kosinin välillä vallitsee yhteys:
sinin ja kosinin välillä vallitsee yhteys: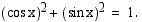
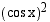 ja
ja 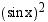 merkitään yleensä ilman sulkeita, jolloin em. tulos saa muodon
merkitään yleensä ilman sulkeita, jolloin em. tulos saa muodon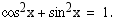
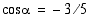 ja
ja 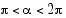 . Määrää
. Määrää 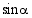 ja
ja  .
.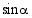 Pythagoraan lauseen avulla.
Pythagoraan lauseen avulla.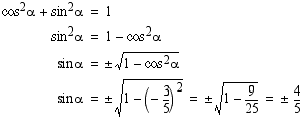
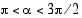 . Tällöin
. Tällöin 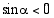 eli nyt
eli nyt 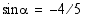 .
.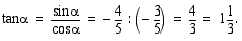
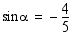 ja
ja 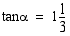
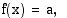
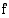 on jokin trigonometrinen funktio ja
on jokin trigonometrinen funktio ja 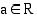 . Koska sini, kosini ja tangentti saavat jaksollisina funktioina jokaisen arvonsa äärettömän monta kertaa, trigonometrisilla yhtälöillä on yleensä äärettömän monta ratkaisua.
. Koska sini, kosini ja tangentti saavat jaksollisina funktioina jokaisen arvonsa äärettömän monta kertaa, trigonometrisilla yhtälöillä on yleensä äärettömän monta ratkaisua.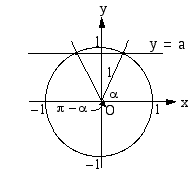 Yhtälöllä
Yhtälöllä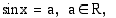
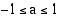 . Tällöin niitä on äärettömän monta. Jos yhtälöllä
. Tällöin niitä on äärettömän monta. Jos yhtälöllä 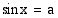 on ratkaisu
on ratkaisu 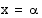 , niin myös
, niin myös  on ratkaisu. Koska sinifunktion perusjakso on
on ratkaisu. Koska sinifunktion perusjakso on 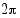 , yhtälön
, yhtälön 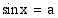 kaikki ratkaisut ovat
kaikki ratkaisut ovat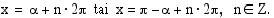
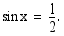
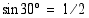 , yhtälön eräs ratkaisu on
, yhtälön eräs ratkaisu on 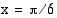 . Tällöin muut ratkaisut ovat
. Tällöin muut ratkaisut ovat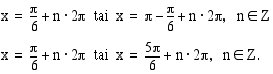
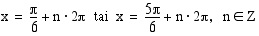
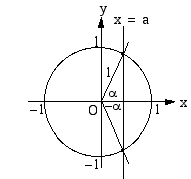 Yhtälöllä
Yhtälöllä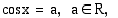
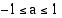 . Jos
. Jos 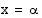 on yhtälön
on yhtälön 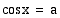 ratkaisu,
ratkaisu, 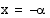 on myös sen ratkaisu. Koska kosinifunktion perusjakso on
on myös sen ratkaisu. Koska kosinifunktion perusjakso on 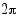 , yhtälön kaikki ratkaisut ovat
, yhtälön kaikki ratkaisut ovat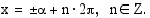
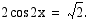
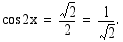
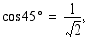
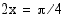 . Yhtälön kaikki ratkaisut ovat
. Yhtälön kaikki ratkaisut ovat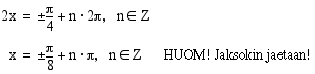
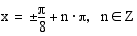
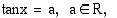
 :n välein. Jos yhtälön
:n välein. Jos yhtälön 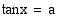 eräs ratkaisu on
eräs ratkaisu on 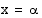 , sen kaikki ratkaisut ovat
, sen kaikki ratkaisut ovat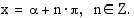
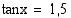 .
.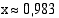 . Yhtälön kaikki ratkaisut ovat
. Yhtälön kaikki ratkaisut ovat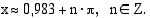
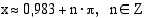
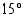
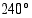
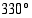
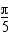
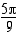
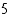
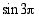
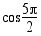
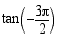
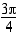 trigonometristen funktioiden arvot.
trigonometristen funktioiden arvot.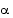 sini on
sini on 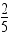 . Määrää sini, kosini ja tangentti kulmalle
. Määrää sini, kosini ja tangentti kulmalle 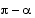 .
. 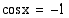
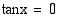
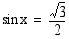 .
.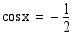
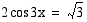
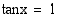
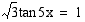
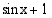
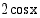
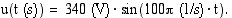
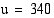 (V).
(V).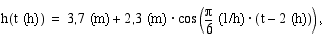
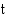 on aika tunteina keskiyöstä 0.00 lukien. Milloin veden korkeus on suurin ja milloin pienin? Laske myös nämä korkeudet.
on aika tunteina keskiyöstä 0.00 lukien. Milloin veden korkeus on suurin ja milloin pienin? Laske myös nämä korkeudet.