4.6.2. Logaritmifunktio
Eksponenttifunktiolla kuvataan suureen kasvamista ajan suhteen. Seuraavaksi selvitetään, kuinka ratkaistaan aika, jonka kuluttua suure on kasvanut (tai vähentynyt) tiettyyn arvoon.
Esimerkki 4.25.
Bakteeri jakautuu kerran tunnissa. Minkä ajan kuluttua bakteereja on jo 7000?
Ratkaisu:
Bakteerien määrä 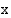 tunnin kuluttua on
tunnin kuluttua on 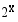 (kpl). On ratkaistava yhtälö
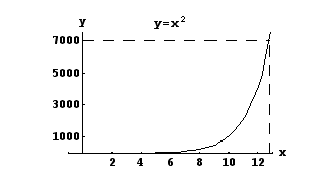
(kpl). On ratkaistava yhtälö 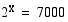 . Koska lukua 7000 ei osata kirjoittaa luvun 2 potenssina, tyydytään graafisesti saatuun likimääräiseen ratkaisuun. Ohessa on funktion
. Koska lukua 7000 ei osata kirjoittaa luvun 2 potenssina, tyydytään graafisesti saatuun likimääräiseen ratkaisuun. Ohessa on funktion 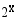 kuvaaja. Sen perusteella yhtälön
kuvaaja. Sen perusteella yhtälön 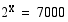 likimääräinen ratkaisu on
likimääräinen ratkaisu on 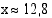 .
.
Vastaus: n. 12,8 tunnin kuluttua.
Huom!
Edellisessä esimerkissä määrätty luku 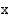 , joka toteuttaa yhtälön
, joka toteuttaa yhtälön 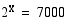 , on luvun 7000 2-kantainen logaritmi, jota merkitään
, on luvun 7000 2-kantainen logaritmi, jota merkitään 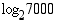 . Se on eksponentti, johon kantaluku 2 on korotettava, jotta saataisiin 7000.
. Se on eksponentti, johon kantaluku 2 on korotettava, jotta saataisiin 7000.
Logaritmin määritelmä ja laskusääntöjä
Luvun 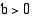
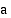 -kantainen logaritmi (
-kantainen logaritmi (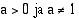 ), jota merkitään
), jota merkitään 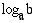 , on eksponentti
, on eksponentti 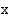 , joka toteuttaa yhtälön
, joka toteuttaa yhtälön 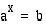 . Luvun
. Luvun 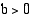
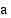 -kantainen logaritmi
-kantainen logaritmi 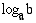 on se kantaluvun
on se kantaluvun 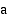 eksponentti, jonka avulla luku
eksponentti, jonka avulla luku 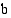 ilmaistaan
ilmaistaan 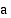 :n potenssina.
:n potenssina.
Logaritmi 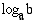 on määritelty ainoastaan positiivisilla luvuilla
on määritelty ainoastaan positiivisilla luvuilla 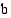 , koska eksponenttifunktio saa vain positiivisia arvoja, ja yhtälöllä
, koska eksponenttifunktio saa vain positiivisia arvoja, ja yhtälöllä 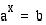 on ratkaisuja vain, kun
on ratkaisuja vain, kun 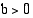 .
.
Esimerkki 4.26.
Laske (a) 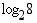 (b)
(b) 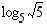 (c)
(c) 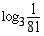
Ratkaisu:
(a)
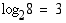 , koska
, koska 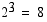 .
.
(b)
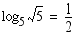 , koska
, koska 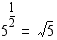
(c)
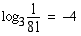 , koska
, koska 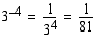
Vastaus: (a) 3 (b) 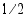 (c)
(c) 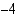
Määritelmän nojalla voidaan osoittaa, että logaritmeille on voimassa seuraavat laskusäännöt: (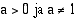 )
)
• 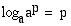
• 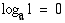 , koska
, koska 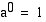
• 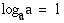 , koska
, koska 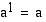
• Kun 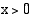 ,
, 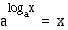 , koska luku
, koska luku 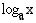 on se kantaluvun
on se kantaluvun 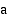 eksponentti, jonka avulla
eksponentti, jonka avulla 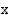 ilmaistaan
ilmaistaan 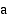 :n potenssina.
:n potenssina.
Esimerkki 4.27.
Laske (a) 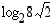 (b)
(b) 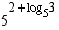 (c)
(c) 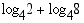
Ratkaisu:
(a)
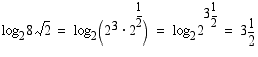
(b)
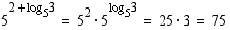
(c)
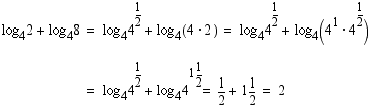
Vastaus: (a) 3,5 (b) 75 (c) 2
Logaritmeille voidaan johtaa vielä seuraavat laskusäännöt, joiden todistukset sivuutetaan tällä kurssilla. (Joissakin säännöissä on logaritmimerkinnästä jätetty kantaluku pois. Kantaluku on näissäkin tapauksissa positiivinen, mutta ei luku yksi.)
• Tulon logaritmi on tekijöiden logaritmien summa:
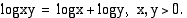
• Osamäärän logaritmi on osoittajan logaritmin ja nimittäjän logaritmin erotus:
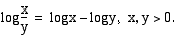
• Potenssin 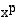 logaritmi on luvun
logaritmi on luvun 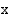 logaritmi kerrottuna eksponentilla
logaritmi kerrottuna eksponentilla 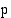 :
:
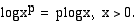
• Luvun 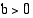
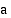 -kantainen logaritmi voidaan ilmoittaa
-kantainen logaritmi voidaan ilmoittaa 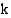 -kantaisina logaritmeina seuraavasti:
-kantaisina logaritmeina seuraavasti:
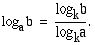
Laskimet sisältävät yleensä 10- ja 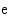 -kantaiset logaritmifunktiot. Näistä 10-kantaista logaritmia kutsutaan
Briggsin logaritmiksi ja sitä merkitään lyhyemmin
-kantaiset logaritmifunktiot. Näistä 10-kantaista logaritmia kutsutaan
Briggsin logaritmiksi ja sitä merkitään lyhyemmin 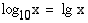 . Logaritmia, jonka kantaluku on Neperin luku
. Logaritmia, jonka kantaluku on Neperin luku 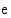 , nimitetään
luonnolliseksi logaritmiksi ja sille käytetään lyhennettä
, nimitetään
luonnolliseksi logaritmiksi ja sille käytetään lyhennettä 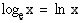 . Muiden logaritmien likiarvoja ei voi laskea suoraan taskulaskimella. Edellä esitellyn luettelon viimeisen laskusäännön nojalla mikä tahansa
. Muiden logaritmien likiarvoja ei voi laskea suoraan taskulaskimella. Edellä esitellyn luettelon viimeisen laskusäännön nojalla mikä tahansa 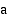 -kantainen logaritmi voidaan kuitenkin ilmoittaa esim. 10-kantaisten tai luonnollisten logaritmien avulla. Tämän jälkeen sen likiarvo saadaan helposti myös taskulaskimella.
-kantainen logaritmi voidaan kuitenkin ilmoittaa esim. 10-kantaisten tai luonnollisten logaritmien avulla. Tämän jälkeen sen likiarvo saadaan helposti myös taskulaskimella.
Esimerkki 4.28.
Laske (a) 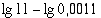 (b)
(b) 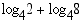
Ratkaisu:
(a)
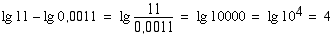
(b)
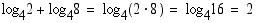
Vastaus: (a) 4 (b) 2
Esimerkki 4.29.
Laske logaritmin 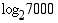 nelidesimaalinen likiarvo.
nelidesimaalinen likiarvo.
Ratkaisu:
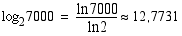
Vastaus: 12,7731
Logaritmifunktion monotonisuus
Monotonisuuden nojalla logaritmifunktiolle on voimassa:
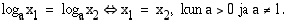
Kun 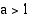 logaritmifunktio on aidosti kasvava ja se säilyttää järjestyksen:
logaritmifunktio on aidosti kasvava ja se säilyttää järjestyksen:
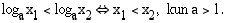
Kun 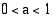 logaritmifunktio aidosti vähenevänä funktiona kääntää järjestyksen:
logaritmifunktio aidosti vähenevänä funktiona kääntää järjestyksen:
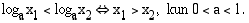
Esimerkki 4.30.
Ratkaise yhtälö 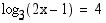 .
.
Ratkaisu:
Yhtälö on määritelty, kun 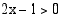 eli kun
eli kun 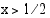 . Logaritmin määritelmän nojalla on oltava voimassa
. Logaritmin määritelmän nojalla on oltava voimassa
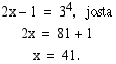
Vastaus: 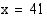
Esimerkki 4.31.
Ratkaise yhtälö 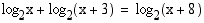 .
.
Ratkaisu:
Yhtälö on määritelty, kun 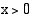 ,
, 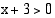 ja
ja 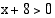 . Nämä ehdot ovat voimassa, kun
. Nämä ehdot ovat voimassa, kun 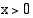 . Kirjoitetaan yhtälön molemmat puolet samankantaisina logaritmeina ja käytetään hyväksi logaritmifunktion monotonisuutta.
. Kirjoitetaan yhtälön molemmat puolet samankantaisina logaritmeina ja käytetään hyväksi logaritmifunktion monotonisuutta.
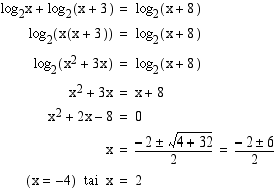
Vastaus: 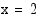
Tarkastellaan lopuksi radioaktiivisen aineen hajoamista esimerkkinä ilmiöstä, jota voidaan kuvata eksponenttifunktiolla.
Radioaktiivisen aineen hajoaminen
Radioaktiiviset aineet hajoavat toisiksi alkuaineiksi tai saman alkuaineen energialtaan pienemmiksi ydinlajeiksi. Hajoamisen nopeutta kuvaa radioaktiivisen aineen
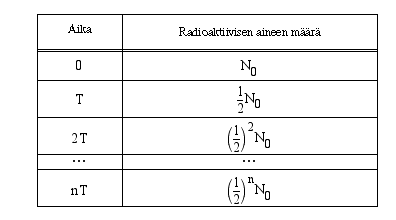
puoliintumisaika 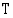 , jonka kuluttua puolet alkuperäisistä radioaktiivisista ytimistä on hajonnut. Puoliintumisaika on kullekin radioaktiiviselle aineelle tyypillinen vakio. Seuraava taulukko näyttää, kuinka radioaktiivisen aineen määrä muuttuu ajan funktiona, kun sen määrä on tarkastelun alkuhetkellä
, jonka kuluttua puolet alkuperäisistä radioaktiivisista ytimistä on hajonnut. Puoliintumisaika on kullekin radioaktiiviselle aineelle tyypillinen vakio. Seuraava taulukko näyttää, kuinka radioaktiivisen aineen määrä muuttuu ajan funktiona, kun sen määrä on tarkastelun alkuhetkellä 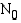 ja aineen puoliintumisaika
ja aineen puoliintumisaika 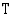 .
.
Määrätään radioaktiivisen aineen määrä mielivaltaisella ajan hetkellä 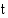 . Merkitään
. Merkitään 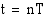 , missä
, missä 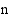 on kuluneinen puoliintumisaikojen lukumäärä. Tällöin
on kuluneinen puoliintumisaikojen lukumäärä. Tällöin 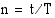 ja edellä olevan taulukkotarkastelun perusteella radioaktiivisen aineen määrä
ja edellä olevan taulukkotarkastelun perusteella radioaktiivisen aineen määrä 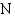 hetkellä
hetkellä 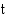 on
on
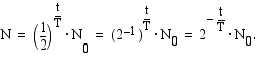
Tämä on radioaktiivisen aineen hajoamislaki.
Esimerkki 4.32.
Radioaktiivisen jodin 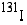 -isotoopin puoliintumisaika on
-isotoopin puoliintumisaika on 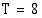 (vrk). Kuinka monta prosenttia ainetta on jäljellä kuukauden ts. 30 (vrk):n kuluttua?
(vrk). Kuinka monta prosenttia ainetta on jäljellä kuukauden ts. 30 (vrk):n kuluttua?
Ratkaisu:
Hajoamislain nojalla aineen määrä on 30 (vrk):n kuluttua
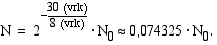
Vastaus: Ainetta on jäljellä 30 (vrk):n kuluttua n. 7,4 %.
Esimerkki 4.33.
Eliön kuollessa lakkaa radioaktiivisen hiilen 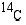 kerääntyminen siihen ja ko. hiili-isotoopin pitoisuus alkaa vähetä. Arkeologi löysi puuesineen, jonka
kerääntyminen siihen ja ko. hiili-isotoopin pitoisuus alkaa vähetä. Arkeologi löysi puuesineen, jonka 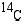 -pitoisuus oli 75 % elävän puun pitoisuudesta. Kuinka vanha esine oli, kun tiedetään, että isotoopin
-pitoisuus oli 75 % elävän puun pitoisuudesta. Kuinka vanha esine oli, kun tiedetään, että isotoopin 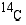 puoliintumisaika on 5600 (v)?
puoliintumisaika on 5600 (v)?
Ratkaisu:
Muodostetaan ensin funktio, joka ilmoittaa 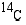 -atomien määrän ajan
-atomien määrän ajan 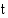 (v) kuluttua. Olkoon radioaktiivisten hiiliatomien määrä aluksi
(v) kuluttua. Olkoon radioaktiivisten hiiliatomien määrä aluksi 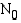 . Ajan
. Ajan 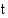 (v) kuluttua
(v) kuluttua 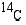 -atomien määrä
-atomien määrä 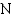 on
on
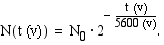
Koska radioaktiivisten hiiliatomien määrä oli 75 % alkuperäisestä, saadaan esineen ikä selville, kun ratkaistaan 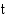 yhtälöstä
yhtälöstä
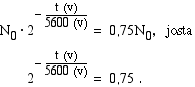
Tämä on eksponenttiyhtälö, jonka ratkaisemiseksi aiemmin esitetty keino ei tepsi, sillä yhtälön molempia puolia ei osata kirjoittaa saman kantaluvun potensseina. Tällaisissa tilanteissa yhtälö saadaan ratkaistua, kun otetaan sen molemmin puolin samankantaiset, esim. luonnolliset logaritmit. Tämä on sallittua, koska yhtälön molemmat puolet ovat positiiviset (logaritmit määriteltyjä), ja logaritmifunktio on aidosti monotoninen (uusi yhtälö on yhtäpitävä eli ekvivalentti alkuperäisen kanssa).
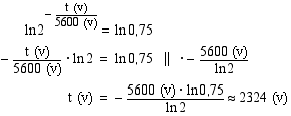
Vastaus: Esine on n. 2300 (v) vanha.
Harjoituksia
36. Olkoon funktio 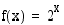 . Laske
. Laske
(a) 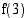
(b) 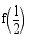
(c) 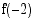
Vastaus tehtävään 36
37. Ratkaise yhtälöt
(a) 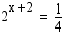
(b) 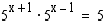
(c) 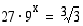
Vastaus tehtävään 37
38. Muovilevy pidättää 20 % siihen tulevasta valosta. Kuinka monta prosenttia valosta pääsee viiden päällekkäin asetetun levyn läpi?
Vastaus tehtävään 38
39. Herra Lahtinen haluaa sijoittaa 45000 (mk) viideksi vuodeksi mahdollisimman tuottavasti. Hänellä on valittavanaan seuraavat vaihtoehdot.
(A) Sijoitetaan koko summa viideksi vuodeksi verottomalle tilille, jonka korkokanta on 2 (%/vuosi). Tilillä korko liitetään pääomaan aina vuoden kuluttua.
(B) Sijoitetaan koko summa viideksi vuodeksi verolliselle tilille, jonka korkokanta on 2,8 (%/vuosi). Korosta peritään jokaisen koronmaksun yhteydessä 28 % lähdeveroa. Tälläkin tilillä korko liitetään pääomaan aina vuoden kuluttua.
(C) Ostetaan ogligaatioita viideksi vuodeksi 45000 (mk):n nimellisarvosta. Kyseinen obligaatiolaina maksetaan takaisin sijoittajalle maksamalla vuosittain 20 % lainan alkuperäisestä nimellisarvosta. Samalla maksetaan lähdeveron (28 %) alainen korko jäljellä olevalle lainalle. Obligaatioiden korkokanta on 5,2 (%/vuosi).
Laske kunkin sijoitusvaihtoehdon korkotuotto.
Vastaus tehtävään 39
40. Tshernobylin ydinvoimalaonnettomuudessa 26.4.1986 vapautui radioaktiivisia cesium-isotooppeja 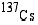 ja
ja 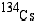 . Niiden puoliintumisajat ovat 30 (v) ja 2,1 (v). Kuinka monta prosenttia ko. isotooppeja oli jäljellä vuoden 1997 huhtikuun lopulla?
. Niiden puoliintumisajat ovat 30 (v) ja 2,1 (v). Kuinka monta prosenttia ko. isotooppeja oli jäljellä vuoden 1997 huhtikuun lopulla?
Vastaus tehtävään 40
41. Yrityksen myynti kasvaa vuosittain 4 %. Tällä hetkellä myynti on 285 (Mmk/v). Muodosta funktio, joka ilmoittaa vuosittaisen myynnin 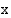 (v) kuluttua nykyhetkestä. Kuinka suuri myynti olisi viiden vuoden kuluttua? Entä kuinka suuri myynti oli 4 (v) sitten, kun oletetaan kasvun pysyneen koko ajan samanlaisena?
(v) kuluttua nykyhetkestä. Kuinka suuri myynti olisi viiden vuoden kuluttua? Entä kuinka suuri myynti oli 4 (v) sitten, kun oletetaan kasvun pysyneen koko ajan samanlaisena?
Vastaus tehtävään 41
42. Laske
(a) 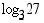
(b) 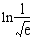
(c) 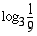
(d) 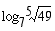
(e) 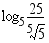
Vastaus tehtävään 42
43. Laske
(a) 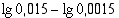
(b) 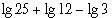
(c) 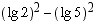
Vastaus tehtävään 43
44. Ratkaise yhtälöt
(a) 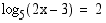
(b) 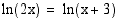
Vastaus tehtävään 44
45. Ratkaise yhtälö 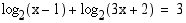 .
.
Vastaus tehtävään 45
46. Ydinonnettomuudessa vapautui radioaktiivista cesiumia 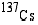 , jonka puoliintumisaika on 30 (v). Mittauksissa todettiin cesiumpitoisuuden olevan kymmenkertainen verrattuna vaarattomana pidettyyn määrään. Kuinka pitkän ajan kuluttua pitoisuus alittaa kyseisen rajan?
, jonka puoliintumisaika on 30 (v). Mittauksissa todettiin cesiumpitoisuuden olevan kymmenkertainen verrattuna vaarattomana pidettyyn määrään. Kuinka pitkän ajan kuluttua pitoisuus alittaa kyseisen rajan?
Vastaus tehtävään 46
47. Mari talletti 10000 (mk) verottomalle tilille, jonka korkokanta on 2 (%/vuosi). Tilillä korko liitetään pääomaan aina vuoden kuluttua. Minkä ajan kuluttua tilin saldo ylittäisi ensimmäisen kerran 15000 (mk) olettaen, että tililtä ei nosteta tänä aikana varoja?
Vastaus tehtävään 47
48. Jäihin pudonneen ihmisen kehon lämpötila 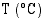
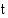 (min) kuluttua putoamisesta on
(min) kuluttua putoamisesta on
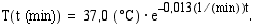
(a) Mikä on kehon lämpötila viiden minuutin kuluttua putoamisesta?
(b) Milloin lämpötila on laskenut 27 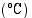 :een?
:een?
Vastaus tehtävään 48
49. Maanjäristyksen voimakkuutta kuvataan Richterin asteikolla. Jos järistyksestä vapautuvan energian määrä megawattitunteina (MWh) on 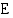 , järistyksen voimakkuus
, järistyksen voimakkuus 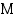 richtereinä on
richtereinä on 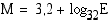 . Keski-Italiaa vavisutti 3.10.1997 maanjäristys, jonka voimakkuudeksi mitattiin 4,7 richteriä. Laske järistyksessä vapautuneen energian määrä. Loviisan ydinvoimala tuottaa energiaa 880 (MWh/h). Kuinka suuressa ajassa se tuottaa saman energiamäärän kuin Keski-Italian järistys?
. Keski-Italiaa vavisutti 3.10.1997 maanjäristys, jonka voimakkuudeksi mitattiin 4,7 richteriä. Laske järistyksessä vapautuneen energian määrä. Loviisan ydinvoimala tuottaa energiaa 880 (MWh/h). Kuinka suuressa ajassa se tuottaa saman energiamäärän kuin Keski-Italian järistys?
Vastaus tehtävään 49
50. Työnnettäessä savolaismallinen vene sopivalla voimalla tyynelle järven selälle, riippuu veneen kulkema matka 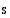 (m) ajasta
(m) ajasta 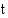 (s) noudattaen seuraavaa funktiota
(s) noudattaen seuraavaa funktiota
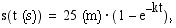
missä 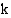
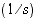 on ns. venevakio. Työntöhetkellä aika
on ns. venevakio. Työntöhetkellä aika 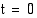 (s). Kun aikaa on kulunut 6,0 (s), vene on lipunut 10,0 (m).
(s). Kun aikaa on kulunut 6,0 (s), vene on lipunut 10,0 (m).
(a) Kuinka pitkän matkan vene on kulkenut 20,0 (s):ssa?
(b) Milloin vene on kulkenut 24,0 (m)?
Vastaus tehtävään 50
51. Pankkivirkailija löydettiin murhattuna klo 12.30 hyvin ilmastoidusta pankista. Ruumiin lämpötila oli löytöhetkellä 31,3 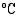 . Tiedetään, että ruumiin lämpötila
. Tiedetään, että ruumiin lämpötila 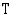 noudattaa funktiota
noudattaa funktiota 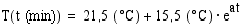 , missä
, missä 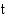 on aika minuutteina murhahetkestä ja vakio
on aika minuutteina murhahetkestä ja vakio 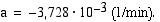 Auta tapausta tutkivaa tarkastaja Kettunivaa ja laske, milloin murha oli tapahtunut.
Auta tapausta tutkivaa tarkastaja Kettunivaa ja laske, milloin murha oli tapahtunut.
Vastaus tehtävään 51
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
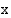 tunnin kuluttua on
tunnin kuluttua on 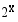 (kpl). On ratkaistava yhtälö
(kpl). On ratkaistava yhtälö 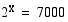 . Koska lukua 7000 ei osata kirjoittaa luvun 2 potenssina, tyydytään graafisesti saatuun likimääräiseen ratkaisuun. Ohessa on funktion
. Koska lukua 7000 ei osata kirjoittaa luvun 2 potenssina, tyydytään graafisesti saatuun likimääräiseen ratkaisuun. Ohessa on funktion 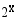 kuvaaja. Sen perusteella yhtälön
kuvaaja. Sen perusteella yhtälön 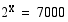 likimääräinen ratkaisu on
likimääräinen ratkaisu on 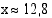 .
. 
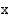 , joka toteuttaa yhtälön
, joka toteuttaa yhtälön 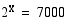 , on luvun 7000 2-kantainen logaritmi, jota merkitään
, on luvun 7000 2-kantainen logaritmi, jota merkitään 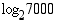 . Se on eksponentti, johon kantaluku 2 on korotettava, jotta saataisiin 7000.
. Se on eksponentti, johon kantaluku 2 on korotettava, jotta saataisiin 7000.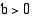
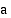 -kantainen logaritmi
-kantainen logaritmi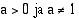 ), jota merkitään
), jota merkitään 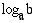 , on eksponentti
, on eksponentti 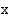 , joka toteuttaa yhtälön
, joka toteuttaa yhtälön 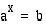 . Luvun
. Luvun 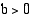
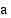 -kantainen logaritmi
-kantainen logaritmi 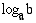 on se kantaluvun
on se kantaluvun 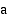 eksponentti, jonka avulla luku
eksponentti, jonka avulla luku 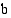 ilmaistaan
ilmaistaan 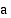 :n potenssina.
:n potenssina. 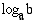 on määritelty ainoastaan positiivisilla luvuilla
on määritelty ainoastaan positiivisilla luvuilla 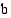 , koska eksponenttifunktio saa vain positiivisia arvoja, ja yhtälöllä
, koska eksponenttifunktio saa vain positiivisia arvoja, ja yhtälöllä 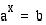 on ratkaisuja vain, kun
on ratkaisuja vain, kun 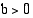 .
.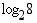 (b)
(b) 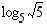 (c)
(c) 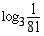
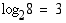 , koska
, koska 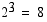 .
.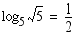 , koska
, koska 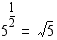
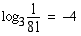 , koska
, koska 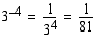
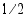 (c)
(c) 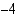
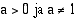 )
)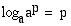
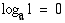 , koska
, koska 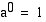
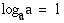 , koska
, koska 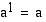
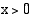 ,
, 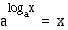 , koska luku
, koska luku 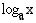 on se kantaluvun
on se kantaluvun 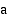 eksponentti, jonka avulla
eksponentti, jonka avulla 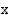 ilmaistaan
ilmaistaan 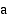 :n potenssina.
:n potenssina.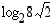 (b)
(b) 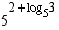 (c)
(c) 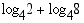
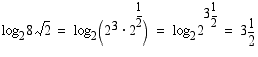
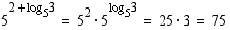
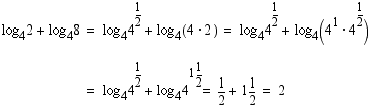
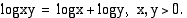
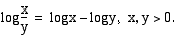
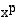 logaritmi on luvun
logaritmi on luvun 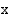 logaritmi kerrottuna eksponentilla
logaritmi kerrottuna eksponentilla 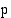 :
: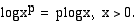
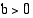
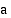 -kantainen logaritmi voidaan ilmoittaa
-kantainen logaritmi voidaan ilmoittaa 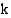 -kantaisina logaritmeina seuraavasti:
-kantaisina logaritmeina seuraavasti: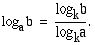
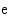 -kantaiset logaritmifunktiot. Näistä 10-kantaista logaritmia kutsutaan
Briggsin logaritmiksi
-kantaiset logaritmifunktiot. Näistä 10-kantaista logaritmia kutsutaan
Briggsin logaritmiksi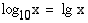 . Logaritmia, jonka kantaluku on Neperin luku
. Logaritmia, jonka kantaluku on Neperin luku 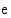 , nimitetään
luonnolliseksi logaritmiksi
, nimitetään
luonnolliseksi logaritmiksi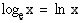 . Muiden logaritmien likiarvoja ei voi laskea suoraan taskulaskimella. Edellä esitellyn luettelon viimeisen laskusäännön nojalla mikä tahansa
. Muiden logaritmien likiarvoja ei voi laskea suoraan taskulaskimella. Edellä esitellyn luettelon viimeisen laskusäännön nojalla mikä tahansa 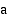 -kantainen logaritmi voidaan kuitenkin ilmoittaa esim. 10-kantaisten tai luonnollisten logaritmien avulla. Tämän jälkeen sen likiarvo saadaan helposti myös taskulaskimella.
-kantainen logaritmi voidaan kuitenkin ilmoittaa esim. 10-kantaisten tai luonnollisten logaritmien avulla. Tämän jälkeen sen likiarvo saadaan helposti myös taskulaskimella.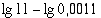 (b)
(b) 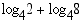
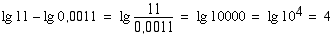
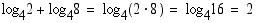
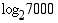 nelidesimaalinen likiarvo.
nelidesimaalinen likiarvo.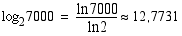
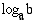 on se muuttujan arvo, jolla eksponenttifunktio
on se muuttujan arvo, jolla eksponenttifunktio 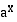 saa arvon
saa arvon 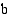 , logaritmifunktio
, logaritmifunktio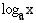 (
(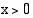 ) on eksponenttifunktion
) on eksponenttifunktion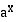 (
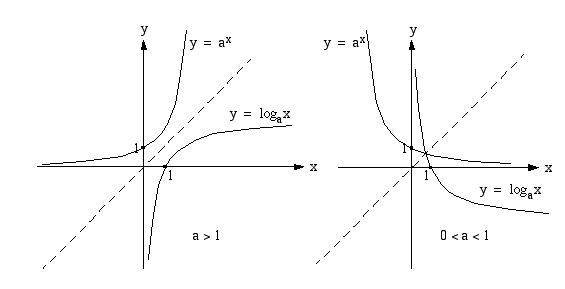
(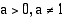 ) käänteisfunktio. Oheiseen kuvaan on piirretty näiden funktioiden kuvaajat, jotka ovat symmetriset suoran
) käänteisfunktio. Oheiseen kuvaan on piirretty näiden funktioiden kuvaajat, jotka ovat symmetriset suoran 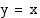 suhteen.
suhteen.
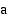 arvosta seuraavasti:
arvosta seuraavasti: 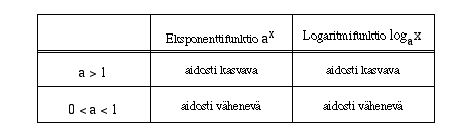
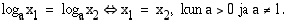
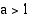 logaritmifunktio on aidosti kasvava ja se säilyttää järjestyksen:
logaritmifunktio on aidosti kasvava ja se säilyttää järjestyksen: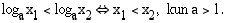
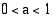 logaritmifunktio aidosti vähenevänä funktiona kääntää järjestyksen:
logaritmifunktio aidosti vähenevänä funktiona kääntää järjestyksen: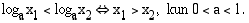
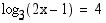 .
.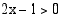 eli kun
eli kun 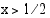 . Logaritmin määritelmän nojalla on oltava voimassa
. Logaritmin määritelmän nojalla on oltava voimassa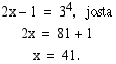
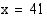
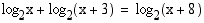 .
.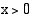 ,
, 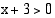 ja
ja 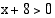 . Nämä ehdot ovat voimassa, kun
. Nämä ehdot ovat voimassa, kun 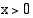 . Kirjoitetaan yhtälön molemmat puolet samankantaisina logaritmeina ja käytetään hyväksi logaritmifunktion monotonisuutta.
. Kirjoitetaan yhtälön molemmat puolet samankantaisina logaritmeina ja käytetään hyväksi logaritmifunktion monotonisuutta.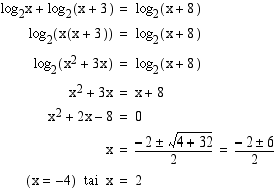
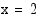
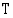 , jonka kuluttua puolet alkuperäisistä radioaktiivisista ytimistä on hajonnut. Puoliintumisaika on kullekin radioaktiiviselle aineelle tyypillinen vakio. Seuraava taulukko näyttää, kuinka radioaktiivisen aineen määrä muuttuu ajan funktiona, kun sen määrä on tarkastelun alkuhetkellä
, jonka kuluttua puolet alkuperäisistä radioaktiivisista ytimistä on hajonnut. Puoliintumisaika on kullekin radioaktiiviselle aineelle tyypillinen vakio. Seuraava taulukko näyttää, kuinka radioaktiivisen aineen määrä muuttuu ajan funktiona, kun sen määrä on tarkastelun alkuhetkellä 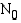 ja aineen puoliintumisaika
ja aineen puoliintumisaika  .
. 
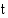 . Merkitään
. Merkitään 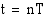 , missä
, missä 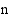 on kuluneinen puoliintumisaikojen lukumäärä. Tällöin
on kuluneinen puoliintumisaikojen lukumäärä. Tällöin 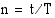 ja edellä olevan taulukkotarkastelun perusteella radioaktiivisen aineen määrä
ja edellä olevan taulukkotarkastelun perusteella radioaktiivisen aineen määrä 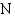 hetkellä
hetkellä 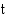 on
on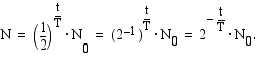
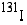 -isotoopin puoliintumisaika on
-isotoopin puoliintumisaika on 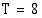 (vrk). Kuinka monta prosenttia ainetta on jäljellä kuukauden ts. 30 (vrk):n kuluttua?
(vrk). Kuinka monta prosenttia ainetta on jäljellä kuukauden ts. 30 (vrk):n kuluttua?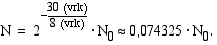
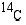 kerääntyminen siihen ja ko. hiili-isotoopin pitoisuus alkaa vähetä. Arkeologi löysi puuesineen, jonka
kerääntyminen siihen ja ko. hiili-isotoopin pitoisuus alkaa vähetä. Arkeologi löysi puuesineen, jonka 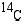 -pitoisuus oli 75 % elävän puun pitoisuudesta. Kuinka vanha esine oli, kun tiedetään, että isotoopin
-pitoisuus oli 75 % elävän puun pitoisuudesta. Kuinka vanha esine oli, kun tiedetään, että isotoopin 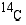 puoliintumisaika on 5600 (v)?
puoliintumisaika on 5600 (v)? 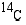 -atomien määrän ajan
-atomien määrän ajan 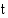 (v) kuluttua. Olkoon radioaktiivisten hiiliatomien määrä aluksi
(v) kuluttua. Olkoon radioaktiivisten hiiliatomien määrä aluksi 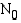 . Ajan
. Ajan 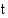 (v) kuluttua
(v) kuluttua 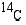 -atomien määrä
-atomien määrä 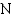 on
on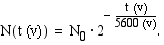
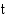 yhtälöstä
yhtälöstä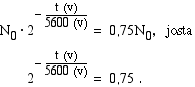
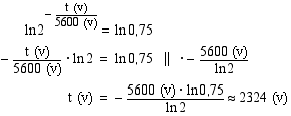
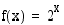 . Laske
. Laske 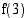
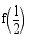
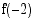
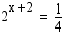
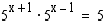
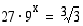
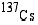 ja
ja 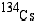 . Niiden puoliintumisajat ovat 30 (v) ja 2,1 (v). Kuinka monta prosenttia ko. isotooppeja oli jäljellä vuoden 1997 huhtikuun lopulla?
. Niiden puoliintumisajat ovat 30 (v) ja 2,1 (v). Kuinka monta prosenttia ko. isotooppeja oli jäljellä vuoden 1997 huhtikuun lopulla?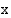 (v) kuluttua nykyhetkestä. Kuinka suuri myynti olisi viiden vuoden kuluttua? Entä kuinka suuri myynti oli 4 (v) sitten, kun oletetaan kasvun pysyneen koko ajan samanlaisena?
(v) kuluttua nykyhetkestä. Kuinka suuri myynti olisi viiden vuoden kuluttua? Entä kuinka suuri myynti oli 4 (v) sitten, kun oletetaan kasvun pysyneen koko ajan samanlaisena?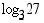
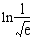
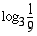
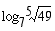
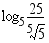
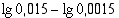
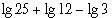
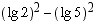
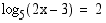
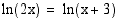
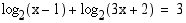 .
.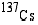 , jonka puoliintumisaika on 30 (v). Mittauksissa todettiin cesiumpitoisuuden olevan kymmenkertainen verrattuna vaarattomana pidettyyn määrään. Kuinka pitkän ajan kuluttua pitoisuus alittaa kyseisen rajan?
, jonka puoliintumisaika on 30 (v). Mittauksissa todettiin cesiumpitoisuuden olevan kymmenkertainen verrattuna vaarattomana pidettyyn määrään. Kuinka pitkän ajan kuluttua pitoisuus alittaa kyseisen rajan?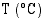
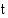 (min) kuluttua putoamisesta on
(min) kuluttua putoamisesta on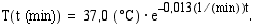
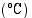 :een?
:een?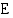 , järistyksen voimakkuus
, järistyksen voimakkuus 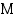 richtereinä on
richtereinä on 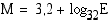 . Keski-Italiaa vavisutti 3.10.1997 maanjäristys, jonka voimakkuudeksi mitattiin 4,7 richteriä. Laske järistyksessä vapautuneen energian määrä. Loviisan ydinvoimala tuottaa energiaa 880 (MWh/h). Kuinka suuressa ajassa se tuottaa saman energiamäärän kuin Keski-Italian järistys?
. Keski-Italiaa vavisutti 3.10.1997 maanjäristys, jonka voimakkuudeksi mitattiin 4,7 richteriä. Laske järistyksessä vapautuneen energian määrä. Loviisan ydinvoimala tuottaa energiaa 880 (MWh/h). Kuinka suuressa ajassa se tuottaa saman energiamäärän kuin Keski-Italian järistys?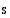 (m) ajasta
(m) ajasta 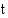 (s) noudattaen seuraavaa funktiota
(s) noudattaen seuraavaa funktiota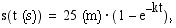
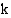
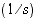 on ns. venevakio. Työntöhetkellä aika
on ns. venevakio. Työntöhetkellä aika 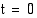 (s). Kun aikaa on kulunut 6,0 (s), vene on lipunut 10,0 (m).
(s). Kun aikaa on kulunut 6,0 (s), vene on lipunut 10,0 (m). 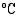 . Tiedetään, että ruumiin lämpötila
. Tiedetään, että ruumiin lämpötila 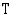 noudattaa funktiota
noudattaa funktiota 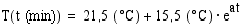 , missä
, missä 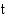 on aika minuutteina murhahetkestä ja vakio
on aika minuutteina murhahetkestä ja vakio 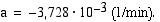 Auta tapausta tutkivaa tarkastaja Kettunivaa ja laske, milloin murha oli tapahtunut.
Auta tapausta tutkivaa tarkastaja Kettunivaa ja laske, milloin murha oli tapahtunut.