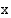 vuoden kuluttua vuodesta 1994 laskettuna.
vuoden kuluttua vuodesta 1994 laskettuna.
Vuonna 1994 Argentiinan väkiluku oli 34,2 (milj.). Sen on havaittu kasvavan keskimäärin 1,4 % vuodessa. Muodosta funktio, joka ilmoittaa ennusteen Argentiinan väkuluvulle 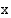 vuoden kuluttua vuodesta 1994 laskettuna.
vuoden kuluttua vuodesta 1994 laskettuna.
Ilmoittakoon 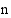 , monesko vuosi vuodesta 1994 lukien on tarkastelussa.
, monesko vuosi vuodesta 1994 lukien on tarkastelussa.
Taulukoidaan Argentiinan väkiluku eri 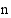 :n arvoilla.
:n arvoilla.

Vastaus: Argentiinan väkiluku 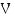 (milj. henkilöä)
(milj. henkilöä) 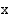 vuoden kuluttua vuodesta 1994 laskettuna on
vuoden kuluttua vuodesta 1994 laskettuna on 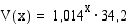 (milj. henkilöä).
(milj. henkilöä).
Edellisen esimerkkifunktion muuttuja (vuosien lukumäärä) esiintyi eksponentissa ja funktiota kutsutaan tästä syystä eksponenttifunktioksi.
missä kantaluku 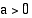 ja se on vakio. Eksponenttifunktio on määritelty kaikilla
ja se on vakio. Eksponenttifunktio on määritelty kaikilla 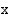 :n reaaliarvoilla, koska kantaluvun ollessa positiivinen voi eksponenttina olla mikä tahansa reaaliluku. Funktion monotonisuus riippuu kantaluvusta
:n reaaliarvoilla, koska kantaluvun ollessa positiivinen voi eksponenttina olla mikä tahansa reaaliluku. Funktion monotonisuus riippuu kantaluvusta 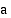 seuraavasti:
seuraavasti:
• Kun 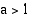 , eksponenttifunktio
, eksponenttifunktio 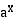 on aidosti kasvava.
on aidosti kasvava.
• Kun 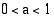 , eksponenttifunktio
, eksponenttifunktio 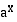 on aidosti vähenevä.
on aidosti vähenevä.
Kummassakin tapauksessa eksponenttifunktion arvojoukko on positiivisten reaalilukujen joukko 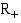 .
.
Eksponenttifunktio on aidosti monotoninen, kun 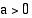 ja
ja  . Monotonisuuden nojalla eksponenttifunktiolle on voimassa
. Monotonisuuden nojalla eksponenttifunktiolle on voimassa
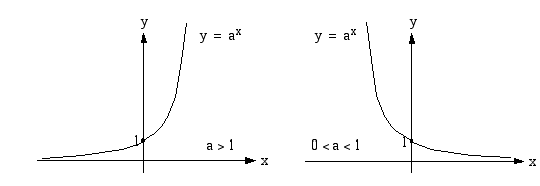
Kirjoitetaan yhtälön molemmat puolet luvun 3 potensseina ja käytetään hyväksi funktion 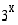 monotonisuutta.
monotonisuutta.
Kun kantaluku 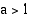 , eksponenttifunktio
, eksponenttifunktio 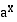 on aidosti kasvava ja se
säilyttää järjestyksen. On siis voimassa
on aidosti kasvava ja se
säilyttää järjestyksen. On siis voimassa
Kirjoitetaan epäyhtälön molemmat puolet luvun 2 potensseina ja käytetään hyväksi tietoa, että aidosti kasvavana funktiona 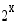 säilyttää järjestyksen.
säilyttää järjestyksen.
Kun kantaluvulle 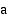 on voimassa
on voimassa 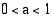 , eksponenttifunktio
, eksponenttifunktio 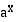 aidosti vähenevänä funktiona
kääntää järjestyksen, jolloin on voimassa
aidosti vähenevänä funktiona
kääntää järjestyksen, jolloin on voimassa
Kuten aiemmissakin esimerkeissä kirjoitetaan epäyhtälön molemmat puolet saman kantaluvun potensseina ja käytetään hyväksi eksponenttifunktion monotonisuutta.
Taskulaskimissa on yleensä valmiina eksponenttifunktiot 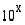 ja
ja 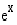 , missä kantaluku
, missä kantaluku 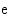 on ns. Neperin luku. Se on irrationaaliluku, jonka likiarvo on 2,71828. Eksponenttifunktiota käytetään matemaattisena mallina kuvattaessa ilmiöitä, joissa yksikköä kohden laskettu kasvu- tai vähenemisnopeus on vakio. Jos siis suure tulee esim. 2- tai 5-kertaiseksi aina vakioajassa tai se kasvaa (vähenee) tietyn prosenttimäärän aina samassa ajassa, sen kasvamista (vähenemistä) voidaan kuvata eksponenttifunktiolla. Tällaisia ilmiöitä ovat esim. saldon kasvu tilillä, jonka korko pysyy vakiona, väestönkasvu, radioaktiivisen aineen hajoaminen, kappaleen jäähtyminen jne.
on ns. Neperin luku. Se on irrationaaliluku, jonka likiarvo on 2,71828. Eksponenttifunktiota käytetään matemaattisena mallina kuvattaessa ilmiöitä, joissa yksikköä kohden laskettu kasvu- tai vähenemisnopeus on vakio. Jos siis suure tulee esim. 2- tai 5-kertaiseksi aina vakioajassa tai se kasvaa (vähenee) tietyn prosenttimäärän aina samassa ajassa, sen kasvamista (vähenemistä) voidaan kuvata eksponenttifunktiolla. Tällaisia ilmiöitä ovat esim. saldon kasvu tilillä, jonka korko pysyy vakiona, väestönkasvu, radioaktiivisen aineen hajoaminen, kappaleen jäähtyminen jne.
Talletetaan 2000 (mk) tilille, jonka korkokanta on 2 (%/vuosi) ja jolla korko liitetään pääomaan jatkuvasti (ei siis vuosittain tai puolivuosittain tai päivittäin). [ Jatkuva-aikaista korkolaskentaa tarvitaan jatkuva-aikaisten taloustieteen teorioiden muodostamiseen. Tietyllä logaritmimuunnoksella jatkuva-aikainen korkolaskenta saadaan vastaamaan tarkasti reaalimaailmassa käytettyä diskreettiä korkolaskentaa. ]
Tiedetään, että tilin saldo 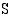 (mk)
(mk) 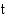 vuoden kuluttua talletuksesta noudattaa tällöin funktiota
vuoden kuluttua talletuksesta noudattaa tällöin funktiota
Laske tilin saldo kolmen vuoden talletuksen jälkeen.
Lääketieteen varjoainekuvauksissa käytetään esim. fluorin radioaktiivista isotooppia 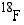 . Aineesta hajoaa 32 % tunnissa. Potilaalle annettiin 2,8 (mg) ko. isotooppia. Muodosta funktio, joka ilmoittaa aineen määrän
. Aineesta hajoaa 32 % tunnissa. Potilaalle annettiin 2,8 (mg) ko. isotooppia. Muodosta funktio, joka ilmoittaa aineen määrän 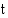 (h) kuluttua sen antamishetkestä laskettuna.
(h) kuluttua sen antamishetkestä laskettuna.
(a) Kuinka paljon ainetta on jäljellä 3 (h) kuluttua?
(b) Potilaan annos valmistettiin 45 (min) ennen sen antamista. Kuinka paljon se sisälsi ainetta?
Koska aineesta hajoaa joka tunti 32 %, siitä jää jäljelle 68 %. Aineen määrä tulee siis joka tunti 0,68-kertaiseksi. Seuraava taulukko näyttää, kuinka radioaktiivisen fluorin määrä muuttuu ajan funktiona.

Olkoon radioaktiivisen fluorin antamishetkestä kulunut mielivaltainen aika 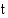 (h). Tällöin antamishetkestä kuluneiden tuntien lukumäärä
(h). Tällöin antamishetkestä kuluneiden tuntien lukumäärä 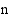 on
on 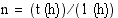 . Radioaktiivisen fluorin määrän
. Radioaktiivisen fluorin määrän 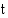 (h) kuluttua antamishetkestä ilmoittaa siten funktio
(h) kuluttua antamishetkestä ilmoittaa siten funktio 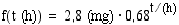 .
.
(a) Aineen määrä 3 (h) kuluttua on
(b) Aineen määrä oli 45 (min) eli 0,75 (h) sitten (ajanhetkenä 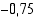 (h))
(h))