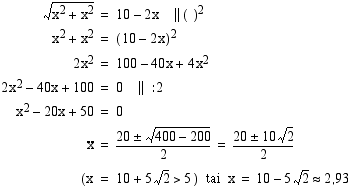2.7.1. Juuriyhtälö
Juuriyhtälö sisältää neliöjuurilausekkeita. Juuriyhtälö ratkaistaan yleensä korottamalla se puolittain neliöön. Neliöönkorotuksella aikaansaatu yhtälö ei kuitenkaan aina ole yhtäpitävä alkuperäisen kanssa: sillä voi olla myös ylimääräisiä ratkaisuja. Koska 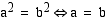 tai
tai 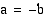 , nämä ylimääräiset ratkaisut toteuttavat jälkimmäisen yhtälön. Sen sijaan, jos
, nämä ylimääräiset ratkaisut toteuttavat jälkimmäisen yhtälön. Sen sijaan, jos 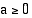 ja
ja 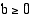 , niin
, niin 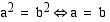 . Tämän perusteella yhtälö (ja epäyhtälö) voidaan korottaa puolittain neliöön, jos sen molemmat puolet ovat ei-negatiiviset. Sääntö on nimeltään
neliöönkorotusehto. Sen ollessa voimassa neliöönkorotuksella aikaansaatu yhtälö (tai epäyhtälö) on yhtäpitävä alkuperäisen kanssa eli niillä on täsmälleen samat ratkaisut.
. Tämän perusteella yhtälö (ja epäyhtälö) voidaan korottaa puolittain neliöön, jos sen molemmat puolet ovat ei-negatiiviset. Sääntö on nimeltään
neliöönkorotusehto. Sen ollessa voimassa neliöönkorotuksella aikaansaatu yhtälö (tai epäyhtälö) on yhtäpitävä alkuperäisen kanssa eli niillä on täsmälleen samat ratkaisut.
Esimerkki 2.22.
Ratkaise yhtälö 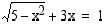 .
.
Ratkaisu:
Neliöönkorotusta varten siirretään ensin termit niin, että juurilauseke jää yksin omalle puolelleen:
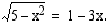
Juurilauseke on määritelty, kun 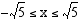 . Koska neliöjuuren arvo on aina positiivinen tai nolla, on lisäksi oltava
. Koska neliöjuuren arvo on aina positiivinen tai nolla, on lisäksi oltava 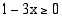 eli
eli 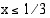 . Molemmat ehdot ovat voimassa, kun
. Molemmat ehdot ovat voimassa, kun 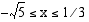 . Tällöin myös yhtälön kummatkin puolet ovat ei-negatiiviset ja se voidaan korottaa puolittain neliöön.
. Tällöin myös yhtälön kummatkin puolet ovat ei-negatiiviset ja se voidaan korottaa puolittain neliöön.
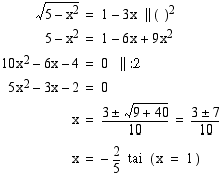
Ainoa ehdon 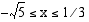 toteuttava ratkaisu on
toteuttava ratkaisu on 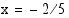 .
.
Vastaus: 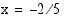
Huom!
Juuriyhtälön voi ratkaista myös korottamalla sen ensin neliöön, ratkaisemalla näin saadun yhtälön ja hylkäämällä saaduista ratkaisuehdokkaista ne, jotka eivät toteuta alkuperäistä yhtälöä.
Esimerkki 2.23.
Neliön muotoisen levyn sivun pituus on 10,0 (cm). Levystä tehdään säännöllinen 8-kulmio poistamalla nurkista palat oheisen kuvan osoittamalla tavalla. Laske, kuinka suuret palat nurkista on poistettava.
Ratkaisu:
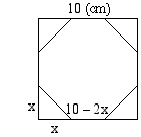 Merkitään poistettavan suorakulmaisen kolmion kateettia
Merkitään poistettavan suorakulmaisen kolmion kateettia 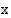 :llä. Tällöin sen hypotenuusa on Pythagoraan lauseen nojalla
:llä. Tällöin sen hypotenuusa on Pythagoraan lauseen nojalla 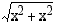 . Kolmioiden poistamisen jälkeen neliön sivusta jäljelle jäävän osan pituus on
. Kolmioiden poistamisen jälkeen neliön sivusta jäljelle jäävän osan pituus on 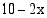 . Koska säännöllisen 8-kulmion kaikki sivut ovat yhtä pitkät, on oltava voimassa
. Koska säännöllisen 8-kulmion kaikki sivut ovat yhtä pitkät, on oltava voimassa 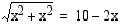 . Ratkaistaan tämä juuriyhtälö korottamalla se puolittain neliöön. Koska tässä tilanteessa on oltava
. Ratkaistaan tämä juuriyhtälö korottamalla se puolittain neliöön. Koska tässä tilanteessa on oltava 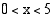 (cm), neliöönkorotusehto on voimassa.
(cm), neliöönkorotusehto on voimassa.
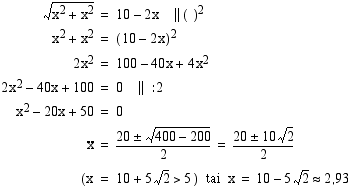
Vastaus: Poistetaan nurkista suorakulmaiset kolmiot, joiden kateetit ovat n. 2,9 (cm). Tällöin 8-kulmion sivun pituus on n. 4,1 (cm).
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
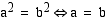 tai
tai 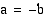 , nämä ylimääräiset ratkaisut toteuttavat jälkimmäisen yhtälön. Sen sijaan, jos
, nämä ylimääräiset ratkaisut toteuttavat jälkimmäisen yhtälön. Sen sijaan, jos 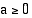 ja
ja 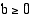 , niin
, niin 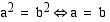 . Tämän perusteella yhtälö (ja epäyhtälö) voidaan korottaa puolittain neliöön, jos sen molemmat puolet ovat ei-negatiiviset. Sääntö on nimeltään
neliöönkorotusehto. Sen ollessa voimassa neliöönkorotuksella aikaansaatu yhtälö (tai epäyhtälö) on yhtäpitävä alkuperäisen kanssa eli niillä on täsmälleen samat ratkaisut.
. Tämän perusteella yhtälö (ja epäyhtälö) voidaan korottaa puolittain neliöön, jos sen molemmat puolet ovat ei-negatiiviset. Sääntö on nimeltään
neliöönkorotusehto. Sen ollessa voimassa neliöönkorotuksella aikaansaatu yhtälö (tai epäyhtälö) on yhtäpitävä alkuperäisen kanssa eli niillä on täsmälleen samat ratkaisut.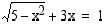 .
.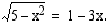
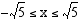 . Koska neliöjuuren arvo on aina positiivinen tai nolla, on lisäksi oltava
. Koska neliöjuuren arvo on aina positiivinen tai nolla, on lisäksi oltava 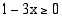 eli
eli 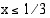 . Molemmat ehdot ovat voimassa, kun
. Molemmat ehdot ovat voimassa, kun 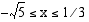 . Tällöin myös yhtälön kummatkin puolet ovat ei-negatiiviset ja se voidaan korottaa puolittain neliöön.
. Tällöin myös yhtälön kummatkin puolet ovat ei-negatiiviset ja se voidaan korottaa puolittain neliöön.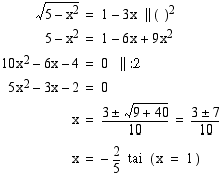
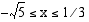 toteuttava ratkaisu on
toteuttava ratkaisu on 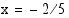 .
.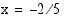
 Merkitään poistettavan suorakulmaisen kolmion kateettia
Merkitään poistettavan suorakulmaisen kolmion kateettia 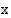 :llä. Tällöin sen hypotenuusa on Pythagoraan lauseen nojalla
:llä. Tällöin sen hypotenuusa on Pythagoraan lauseen nojalla 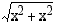 . Kolmioiden poistamisen jälkeen neliön sivusta jäljelle jäävän osan pituus on
. Kolmioiden poistamisen jälkeen neliön sivusta jäljelle jäävän osan pituus on 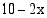 . Koska säännöllisen 8-kulmion kaikki sivut ovat yhtä pitkät, on oltava voimassa
. Koska säännöllisen 8-kulmion kaikki sivut ovat yhtä pitkät, on oltava voimassa 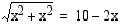 . Ratkaistaan tämä juuriyhtälö korottamalla se puolittain neliöön. Koska tässä tilanteessa on oltava
. Ratkaistaan tämä juuriyhtälö korottamalla se puolittain neliöön. Koska tässä tilanteessa on oltava 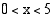 (cm), neliöönkorotusehto on voimassa.
(cm), neliöönkorotusehto on voimassa.