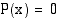 , missä
, missä 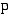 on vähintään kolmatta astetta oleva polynomi. Polynomifunktio on muotoa
on vähintään kolmatta astetta oleva polynomi. Polynomifunktio on muotoa
Korkeamman asteen yhtälö voidaan aina sieventää muotoon 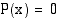 , missä
, missä 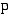 on vähintään kolmatta astetta oleva polynomi. Polynomifunktio on muotoa
on vähintään kolmatta astetta oleva polynomi. Polynomifunktio on muotoa
Korkeamman asteen yhtälön ratkaiseminen perustuu tulon nollasääntöön. Yhtälön vasemman puolen polynomi jaetaan tekijöihin eli se kirjoitetaan korkeintaan toista astetta olevien polynomien tulona. Tämän jälkeen käytetään tulon nollasääntöä: tulo on nolla, jos ja vain jos jokin sen tekijöistä on nolla.
Ryhmitellään polynomin termejä siten, että vasen puoli saadaan tulomuotoon.
Korkeamman asteen yhtälön ratkaisemisen vaikein vaihe on polynomin jakaminen tekijöihin. Edellisen esimerkin kaltainen ryhmittely ei useinkaan onnistu. Polynomi voidaan jakaa tekijöihin nollakohtiensa avulla, jos ne tunnetaan. Jos 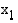 on
on 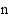 :nnen asteen polynomin
:nnen asteen polynomin
reaalinen nollakohta, jolloin 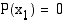 , niin
, niin
missä 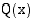 on polynomi, jonka asteluku on
on polynomi, jonka asteluku on 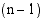 . Toinen tekijäpolynomi
. Toinen tekijäpolynomi 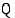 löydetään jakamalla polynomi
löydetään jakamalla polynomi 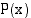 binomilla
binomilla 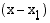 esim. jakokulmassa. Jos
esim. jakokulmassa. Jos 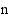 :nnen asteen polynomilla
:nnen asteen polynomilla 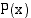 on
on 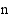 nollakohtaa
nollakohtaa 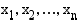 , niin
, niin
Polynomilla, jonka asteluku on 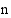 , on enintään
, on enintään 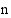 reaalista nollakohtaa, joten
reaalista nollakohtaa, joten 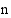 :nnen asteen yhtälöllä
:nnen asteen yhtälöllä 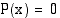 on korkeintaan
on korkeintaan 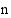 reaalijuurta.
reaalijuurta.
Korkeamman asteen yhtälön ratkaisemiseen tarvittu polynomin jakaminen tekijöihin vaatii siis ainakin yhden nollakohdan löytämistä. Nollakohdan voi onnistua löytämään arvaamalla tai kokeilemalla. Polynomin rationaalisten nollakohtien etsimistä helpottaa seuraava tulos:
Jos kokonaislukukertoimisella yhtälöllä
on rationaalinen ratkaisu 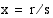 , niin osoittaja
, niin osoittaja 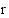 on vakiotermin
on vakiotermin 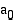 tekijä ja nimittäjä
tekijä ja nimittäjä 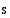 on korkeimman asteen termin kertoimen
on korkeimman asteen termin kertoimen 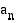 tekijä.
tekijä.
Tulos sopii myös murtolukukertoimisen yhtälön rationaaliratkaisujen etsimiseen. Kun yhtälöstä poistetaan nimittäjät kertomalla se nimittäjien pienimmällä yhteisellä jaettavalla, saadaan alkuperäisen kanssa yhtäpitävä kokonaislukukertoiminen yhtälö.
Kirjoitetaan yhtälö ensin perusmuotoon 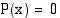 :
:
Jaetaan polynomi tekijöihin etsimällä ensin kokeilemalla yksi yhtälön ratkaisu. Vakiotermin 2 tekijät ovat 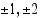 ja kolmannen asteen termin kertoimen 1 tekijät
ja kolmannen asteen termin kertoimen 1 tekijät 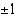 . Mahdolliset rationaalijuuret ovat siten
. Mahdolliset rationaalijuuret ovat siten 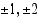 . Kokeilemalla juuriehdokkaita yhtälöön todetaan, että
. Kokeilemalla juuriehdokkaita yhtälöön todetaan, että 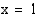 on yksi polynomin nollakohta, sillä
on yksi polynomin nollakohta, sillä
Yksi polynomin tekijä on siten 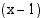 . Suoritetaan jakolasku
. Suoritetaan jakolasku
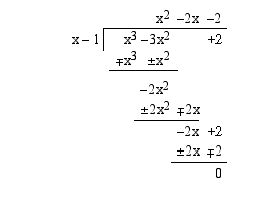
Jakolaskun perusteella yhtälö voidaan esittää muodossa
Ratkaistaan yhtälö tulon nollasäännöllä.
Jaettaessa polynomia 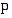 tekijällä
tekijällä 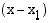 jako menee aina tasan, jos
jako menee aina tasan, jos 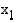 on polynomin
on polynomin 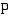 nollakohta eli
nollakohta eli 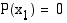 .
.
Eräs erikoistapaus korkeamman asteen yhtälöstä on ns. bikvadraattinen yhtälö. Se on neljännen asteen yhtälö, josta puuttuvat ensimmäisen ja kolmannen asteen termit. Tällainen yhtälö voidaan ratkaista samaan tapaan kuin toisen asteen yhtälö.
Sijoitetaan yhtälöön apumuuttuja 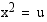 , jolloin saadaan tämän suhteen toisen asteen yhtälö.
, jolloin saadaan tämän suhteen toisen asteen yhtälö.
Palataan takaisin muuttujaan 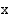 .
.
Kolmannen ja neljännen asteen yhtälöille on olemassa myös omat ratkaisukaavat, mutta ne ovat monimutkaisia. Sen sijaan vähintään viidettä astetta oleville yhtälöille ei voida muodostaa yleisiä ratkaisukaavoja. Tämän todisti norjalainen matemaatikko Niels Abel(1802-1829) 1800-luvun alkupuolella. Jos korkeamman asteen yhtälö ei ratkea kokeiluun ja jaollisuuteen perustuvalla menetelmällä, on tyydyttävä joko graafisesti tai numeerisesti saatuihin likiarvoihin.