2.3.1. Toisen asteen yhtälö

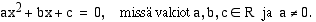
Toisen asteen yhtälö voidaan aina sieventää muotoon

Esimerkki 2.7.

Ratkaise yhtälö .

Ratkaisu:

Vastaus:    tai

Jokainen toisen asteen yhtälö voidaan ratkaista neliöksi täydentämällä. Tällöin yhtälö kirjoitetaan edellisen esimerkin kaltaiseen muotoon, jossa vasempana puolena on binomin neliö ja oikeana puolena jokin luku. Johdetaan toisen asteen yhtälölle yleinen ratkaisukaava soveltamalla tätä menettelyä yhtälöön 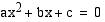, miss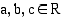ä ja 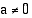. Kerrotaan tämä yhtälö ensin puolittain luvulla 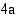ja täydennetään sitten sen vasen puoli neliöksi.

Jos yhtälön vasemmalla puolella olisi lisäksi termi 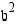, se esittäisi binomin 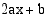neliötä. Lisätään haluttu termi 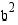yhtälön kummallekin puolelle, jolloin se ei muutu ja vasen puoli saadaan haluttuun muotoon.

Viimeisestä muodosta havaitaan, että yhtälöllä on reaalijuuria, kun 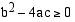. Ratkaistaan nämä juuret.

Tulos on toisen asteen yhtälön ratkaisukaava, jonka avulla voi ratkaista minkä tahansa toisen asteen yhtälön.

Toisen asteen yhtälön ratkaisukaavan juurrettavaa 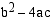sanotaan sen diskriminantiksi ja sitä merkitään yleensä kirjaimella 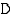. Toisen asteen yhtälön reaaliratkaisujen lukumäärä riippuu diskriminantin arvosta seuravasti:

• Jos 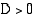, yhtälöllä on kaksi eri reaalijuurta.

• Jos 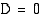, yhtälöllä on yksi ns. kaksoisjuuri.

• Jos 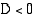, yhtälöllä ei ole reaaliratkaisua. (Yhtälöllä on tällöin kaksi kompleksijuurta.)

Huom!

Koska tällä kurssilla ei käsitellä kompleksilukuja, yhtälöiden ratkaisut etsitään aina reaalilukujen joukosta.

Esimerkki 2.8.

Ratkaise yhtälö .

Ratkaisu:

Vastaus:    tai

Jos toisen asteen yhtälö on vaillinainen siten, että siitä puuttuu vakiotermi, se ratkeaa helpoimmin jakamalla toinen puoli ensin tekijöihin ja käyttämällä tulon nollasääntöä: kahden tai useamman tekijän tulo on nolla, jos ja vain jos jokin sen tekijöistä on nolla.

Esimerkki 2.9.

Ratkaise yhtälö .

Ratkaisu:

Vastaus:    tai

Esimerkki 2.10.

Tiedetään, että tasaisessa liikkeessä (nopeus 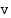vakio) olevan kappaleen kulkema matka 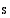on 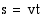, missä 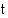on matkaan käytetty aika. Tasaisesti kiihtyvässä liikkeessä (kiihtyvyys 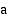vakio) olevan kappaleen ajassa 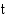kulkema matka on 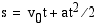ja nopeus 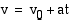, missä 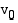on kappaleen alkunopeus. Kun tasaisella nopeudella ajava autoilija havaitsee tiellä esteen, häneltä kuluu 1 (s) reaktioaikaa ennen jarrutusta. Autoilija, joka ajaa nopeudella 50 (km/h) havaitsee tiellä 26 (m):n päässä esteen ja pystyy juuri ja juuri pysähtymään ennen sitä.

(a) Mikä on auton hidastuvuus?

(b) Oletetaan auton hidastuvuus vakioksi samoissa olosuhteissa. Millä nopeudella 70 (km/h) ajava auto törmää 26 (m):n päässä olevaan esteeseen, jos tältäkin autoilijalta kuluu 1 (s) reaktioaikaa ennen jarrutusta?

Ratkaisu:

(a) Auto kulkee reaktioajan vielä tasaisella nopeudella 50 (km/h). Lasketaan ensin reaktiomatka.

Auton jarrurusmatka on

Tämän matkan aikana auton nopeus muuttuu alkunopeudesta 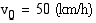loppunopeuteen 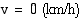. Auton kiihtyvyys (tässä hidastuvuus) voidaan ratkaista jarrutusmatkan kaavasta

Kaavassa on vielä kaksi tuntematonta: kiihtyvyys ja aika. Määrätään ensin jarrutusaika 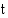kiihtyvyyden avulla. Koska loppunopeus 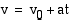, on tästä jarrutusaika

Sijoitetaan tämä jarrutusmatkan kaavaan.

Sijoitetaan tunnetut suureet edellä johdettuun jarrutusmatkan lausekkeeseen ja ratkaistaan kiihtyvyys 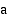saadusta yhtälöstä.

(b) Lasketaan jälleen aluksi reaktiomatka, jonka auto kulkee nopeudella 70 (km/h) yhdessä sekunnissa.

Jarrutusmatkaksi jää tällöin

Edellisessä kohdassa johdetun lausekkeen mukaan jarrutusmatkan 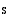ja loppunopeuden 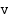välillä on yhteys:

Merkitään loppu- ja alkunopeuden erotusta apumuuttujalla 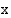ts. 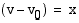. Tällöin saadaan ratkaistavaksi toisen asteen yhtälö muuttujan 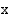suhteen.

Ratkaistaan yhtälöstä.

Sijoitetaan tunnetut suureet ratkaisuun. Muutetaan ensin alkunopeuden 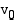yksiköksi (m/s):

.

Koska merkittiin 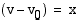, on loppunopeus

Vastaus:   (a) Auton hidastuvuus on n. 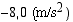   (b) Auton törmäysnopeus on n. 60 (km/h).

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]