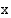 yhtälö on muotoa
yhtälö on muotoa 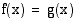 , missä
, missä 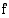 ja
ja 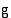 ovat joitakin funktioita. Yhtälöä ratkaistaessa haetaan ne
ovat joitakin funktioita. Yhtälöä ratkaistaessa haetaan ne 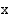 :n arvot, joilla em. yhtäsuuruus on voimassa. Yhtälön ratkaisuja kutsutaan yhtälön
juuriksi.
:n arvot, joilla em. yhtäsuuruus on voimassa. Yhtälön ratkaisuja kutsutaan yhtälön
juuriksi.
Yhden muuttujan 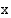 yhtälö on muotoa
yhtälö on muotoa 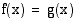 , missä
, missä 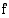 ja
ja 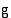 ovat joitakin funktioita. Yhtälöä ratkaistaessa haetaan ne
ovat joitakin funktioita. Yhtälöä ratkaistaessa haetaan ne 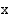 :n arvot, joilla em. yhtäsuuruus on voimassa. Yhtälön ratkaisuja kutsutaan yhtälön
juuriksi.
:n arvot, joilla em. yhtäsuuruus on voimassa. Yhtälön ratkaisuja kutsutaan yhtälön
juuriksi.
Yhtälöä ratkaistaessa voidaan sen lausekkeita sieventää. Tämän lisäksi voidaan yhtälön molempiin puoliin kohdistaa sama toimenpide, joka muuttaa yhtälön kummankin puolen arvoja samalla tavalla eikä muuta yhtälön ratkaisuja.
Koska reaaliluvuille on voimassa seuraavat laskusäännöt:
(1) lisätä yhtälön molemmille puolille sama luku ja
(2) kertoa yhtälön molemmat puolet samalla nollasta eroavalla luvulla
Geometrisesti tulkittuna yhtälön 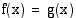 ratkaiseminen merkitsee funktioiden
ratkaiseminen merkitsee funktioiden 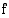 ja
ja 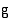 kuvaajien leikkauskohtien etsimistä. Kun yhtälön
kuvaajien leikkauskohtien etsimistä. Kun yhtälön 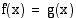 kummallekin puolelle lisätään termi
kummallekin puolelle lisätään termi 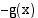 , se saadaan muotoon
, se saadaan muotoon 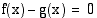 . Siten yhtälön
. Siten yhtälön 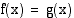 ratkaiseminen voidaan tulkita myös funktion
ratkaiseminen voidaan tulkita myös funktion 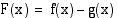 kuvaajan ja
kuvaajan ja 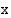 -akselin leikkauskohtien etsimiseksi. Jos käytettävissä on graafinen laskin tai sopiva matemaattinen grafiikkaohjelma, yhtälön likimääräistä ratkaisua voidaan etsiä sen kuvaajaa tarkastelemalla.
-akselin leikkauskohtien etsimiseksi. Jos käytettävissä on graafinen laskin tai sopiva matemaattinen grafiikkaohjelma, yhtälön likimääräistä ratkaisua voidaan etsiä sen kuvaajaa tarkastelemalla.
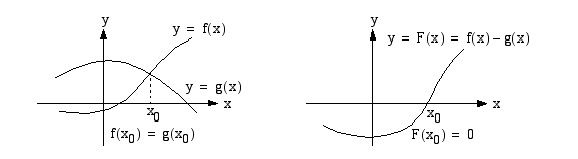
Jos yhtälön ratkaiseminen ei onnistu algebrallisesti eli laskemalla, eikä käytettävissä ole graafiseen ratkaisuun tarvittavaa laitetta, voi yhtälön ratkaista myös numeerisesti. Eri numeeriset menetelmät poikkeavat toisistaan sekä tarvittavien alkutietojen että toimintaperiaatteen suhteen. Yleisimmät yhtälön likimääräiseen ratkaisuun käytetyt numeeriset menetelmät ovat haarukointi, Newtonin menetelmä ja sekanttimenetelmä. Tällä kurssilla ko. menetelmien tarkempi esittely sivuutetaan. Käytännössä myös numeeriset menetelmät vaativat avuksi esim. ohjelmoitavan laskimen tai tietokoneen. Ohjelmoitaviin laskimiin on yleensä jo valmiiksi ohjelmoitu joitakin yhtälöiden numeerisia ratkaisualgoritmeja.