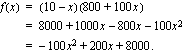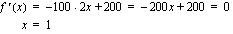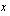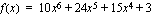[edellinen] [sisällys] [seuraava]
4.4. Derivaatan sovelluksia
Tässä luvussa tutustutaan joihinkin derivaatan sovelluksiin. Päätavoitteemme on oppia tutkimaan funktion kulkua derivaatan avulla.
4.4.1. Funktion kasvaminen ja väheneminen
Tämän asian voit opiskella kokonaan luentomonisteesta. Lue sieltä luku 5.5.1 ja katso huolella esimerkki 5.24. Tämän jälkeen voit harjoitella funktion kasvamisen ja vähenemisen tutkimista derivaatan avulla seuraavalla oppimistehtävällä.
4.4.2. Funktion ääriarvot
Yleinen pyrkimyksemme on optimoida toimintaamme: haluamme esimerkiksi minimoida tuotantokustannuksia ja maksimoida tuottoa tai myyntivoittoa. Erityisesti taloustieteilijän on tärkeää osata ratkaista erilaisia optimointiongelmia. Silloin, kun toimintaa voidaan mallittaa funktion avulla, optimointiongelman ratkaiseminen merkitsee funktion ääriarvojen ja ääriarvokohtien etsimistä. Tätä harjoittelemme seuraavassa derivaatan sovelluksia esittelevässä osiossa.
Tämänkin asian voit opiskella luentomonisteesta. Lue sieltä luvusta 5.5.2, mitä tarkoitetaan funktion ääriarvoilla - minimeillä tai maksimeilla - sekä ääriarvokohdilla, millaisissa kohdissa jatkuvalla funktiolla voi olla lokaali minimi tai maksimi ja kuinka tällaisessa kohdassa voidaan selvittää, onko funktiolla siinä ääriarvoa vai ei. Katso lopuksi huolella esimerkki 5.25, jossa on määrätty derivaatan avulla erään rationaalifunktion ääriarvot.
Tämän jälkeen voit harjoitella funktion ääriarvojen etsimistä oheisen oppimistehtävän avulla.
, 
4.4.3. Funktion suurin ja pienin arvo
Edellä harjoittelimme funktion paikallisten minimi- ja maksimikohtien etsimistä. Optimointiongelmassa halutaan kuitenkin löytää se paras mahdollinen tilanne eli kiinnostuksen kohteena on funktion todellinen suurin tai pienin arvo. Olen luentomonisteessa tarkastellut funktion suurimman ja pienimmän arvon etsimistä erikseen kahdessa eri tilanteessa: ensin suljetulla välillä jatkuvan funktion tapauksessa, sitten yleisemmin muissa tapauksissa.
Luen ensin luentomonisteen luvusta 5.5.3, mitä siellä kerrotaan yleisesti funktion suurimmasta ja pienimmästä arvosta ja kuinka ne löydetään suljetulla välillä jatkuvan funktion tapauksessa. Katso myös esimerkki 5.29, jossa havainnollistetaan tätä ratkaisutapaa.
Koska tiedämme, että suljetulla välillä jatkuvalla funktiolla on aina sekä suurin että pienin arvo, voimme yksinkertaisesti vain etsiä kaikki mahdolliset kohdat, joissa ne voivat olla, ja laskea sitten funktion arvot näissä kohdissa sekä valita lopuksi näistä funktion arvoista suurin ja pienin arvo. Kohtia, joissa suljetulla välillä jatkuvan funktion suurin tai pienin arvo voi olla, ovat välillä olevat derivaatan nollakohdat ja kohdat, joissa funktio ei ole derivoituva (esim. kärkikohdat) sekä välin päätepisteet.
Monissa käytännön tilanteissa muuttuja ei voi saada mitä tahansa arvoja ja tarkastelu voidaan rajata realistisesti jollekin suljetulle välille. Näin tämä erikoistapauksena esitetty tapa määrittää funktion suurin tai pienin arvo soveltuu kuitenkin monien käytännön optimointiongelmien ratkaisemiseen. Tarkastellaan aluksi seuraavaa sovellusesimerkkiä.
Esimerkki 3.10.
Lavatanssien järjestäjät arvioivat, että pääsylipun hinnan ollessa 10 euroa/kpl tansseihin saapuu 800 henkeä. Lisäksi he arvioivat, että pääsylipun hinnan alentaminen 50 sentillä lisää aina yleisöä 50 hengellä. Millä hinnalla tanssien järjestäjät saavat korkeimmat lipputulot? Kuinka suuret ne ovat ja mikä on tällöin yleisömäärä?
Muodostetaan funktio, joka ilmoittaa pääsylipputulot hinnanalennuksen funktiona. Alennetaan lipun hintaa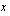 
euroa. Lipun hinta on tällöin 
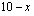euroa. Koska yleisömäärä kasvaa 50 hengellä jokaista puolen euron alennusta kohti, kasvaa se 100 hengellä jokaista euron suuruista hinnanalennusta kohti. Yleisömäärä on tällöin 
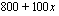. Pääsylipputulot saadaan lipun hinnan ja yleisömäärän tulona eli ne ilmoittaa funktio:
Koska muuttuja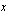 
on nyt pääsylipun hinnanalennus, se ei voi olla negatiivinen eikä myöskään ylittää alkuperäistä hintaa 10 euroa. Tästä syystä funktion 
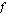määrittelyjoukko on suljettu väli 
.
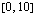Funktio 
on jatkuva suljetulla välillä, joten sillä on suurin arvo. Koska funktio on myös derivoituva, tuo suurin arvo voi olla vain derivaatan nollakohdassa tai välin päätepisteessä. Ratkaistaan ensin derivaatan nollakohdat.
Lasketaan sitten funktion arvo välin päätepisteissä ja edellä löydetyssä derivaatan nollakohdassa.
Pääsylipputulot ovat mahdollisimman suuret, kun lipun hintaa alennetaan yhden euron verran. Hinta on tällöin 9 euroa ja pääsylipputulot 8100 euroa. Yleisöä tansseihin saapuu tuolloin 900 henkeä.
Tarkkaavainen lukija on jo tässä vaiheessa havainnut, että tarkasteltavana olevan funktion kuvaaja on alaspäin aukeava paraabeli. Tällöin funktio saa suurimman arvonsa huipussa eli derivaatan nollakohdassa. Tämän huomion nojalla olisimme edellä voineet välttää funktion arvon laskemisen välin päätepisteissä. On kuitenkin huomattava, että funktion suurimman tai pienimmän arvon olemassaolo tietyssä pisteessä on aina perusteltava jollakin tavalla.
Oppimistehtävä 3.11.
suurin ja pienin arvo välillä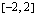 
.
Silloin, kun funktio ei ole määritelty suljetulla välillä tai se ei ole jatkuva, sillä ei välttämättä edes ole suurinta tai pienintä arvoa. Tällöin on vain tutkittava funktion kulkua (sen monotonisuutta ja lokaaleja ääriarvoja) mm. derivaatan ja erilaisten raja-arvotarkastelujen avulla. Tästä tapauksesta on luentomonisteessa esimerkki 5.31. Esimerkki liittyy erääseen rationaalifunktioiden sovellukseen, jota on esitelty jo luvussa 4.4 sivulla 92. Lue ensin tämä esimerkki ja jatka sitten esimerkin 5.31 parissa sivulta 159 alkaen.
Lopuksi voit harjoitella funktion suurimman ja pienimmän arvon etsimistä tällaisessa yleisessä tapauksessa oheisen oppimistehtävän avulla. Muista aina, että näissä tilanteissa emme yleensä edes tiedä etukäteen, onko funktiolla suurinta tai pienintä arvoa.
Testaa tietosi IV
http://www.cc.jyu.fi/~anvihola/testit/testaa/derivtesti2.php
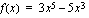
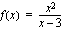