Funktio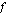 
on derivoituva, joten sillä voi olla lokaali ääriarvo ainoastaan derivaatan nollakohdassa. Määrätään ensin funktion derivaatta.
Funktio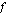
on derivoituva, joten sillä voi olla lokaali ääriarvo ainoastaan derivaatan nollakohdassa. Määrätään ensin funktion derivaatta.
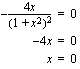
Laaditaan derivaatan merkkikaavio funktion monotonisuuden ja ääriarvon laadun tutkimiseksi. Koska jälleen derivaatan nimittäjä on aina positiivinen, määrää derivaatan osoittaja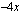 
koko derivaatan merkin. Funktion 
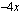kuvaaja on laskeva suora, joten 
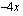saa positiivisia arvoja nollakohtansa vasemmalla ja negatiivisia arvoja sen oikealla puolella. Hyödynnetään tätä tietoa derivaatan merkkikaavion laadinnassa.
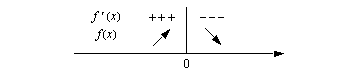
Merkkikaavion perusteella funktiolla on lokaali maksimi ja samalla myös suurin arvo kohdassa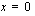 
. Funktion suurin arvo on siten 
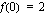. Päätellään vielä, mitä funktion arvoille tapahtuu, kun muuttujan arvot kasvavat tai vähenevät rajatta. Tällöin nimittäjä kasvaa rajatta, mutta osoittaja on koko ajan kaksi, joten osamäärä lähestyy nollaa. Funktion kuvaaja lähestyy siten hyvin suurilla ja hyvin pienillä muuttujan arvoilla 
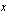-akselia, mutta ei koskaan saavuta sitä. Funktiolla ei siis ole pienintä arvoa.
, pienintä arvoa ei ole