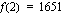Oppimistehtävä 3.11. s. 168

Ratkaisu:

Koska kyseessä on suljetulla välillä jatkuva funktio, sillä on sekä suurin että pienin arvo. Funktio on derivoituva, joten sen suurin tai pienin arvo voi olla ainoastaan derivaatan nollakohdassa tai välin päätepisteessä. Määrätään ensin funktion derivaatta:

.

Ratkaistaan sitten derivaatan nollakohdat.

 

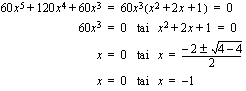
Funktion suurin ja pienin arvo löytyvät nyt joko välin päätepisteistä 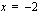tai 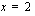tai derivaatan nollakohdista 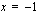tai 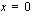. Lasketaan funktion arvot näissä kohdissa ja valitaan niistä suurin ja pienin arvo.

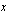
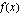
-2	115
-1	4
0	3	pienin arvo
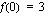2	1651	suurin arvo