Tutkitaan funktion monotonisuutta sen derivaatan avulla. Määrätään ensin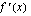 
:
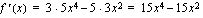. Funktion kasvamista ja vähenemistä on kätevintä tutkia derivaatan merkkikaaviolla. Sitä varten meidän on ensin määrättävä derivaatan nollakohdat.
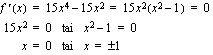
Derivaatan merkkikaavioon varataan oma rivi derivaatan eri tekijöille, derivaatalle, joka on tässä kyseisten tekijöiden tulo, sekä itse funktiolle. Kaavioon merkitään pystyviiva jokaiseen kohtaan, jossa derivaatta voi vaihtaa merkkiään. Tässä noita kohtia ovat edellä löydetyt derivaatan nollakohdat. Mikäli funktiolla on kohtia, joissa se ei ole derivoituva, on nuo kohdat myös merkittävä derivaatan merkkikaavioon. Tämän jälkeen kaavioon merkitään symboleita + ja - käyttäen derivaatan eri tekijöiden merkit eri väleillä. Muista jälleen, että tietyllä välillä näin laaditussa kaaviossa tekijä saa joko vain positiivisia tai vain negatiivisia arvoja. Mikäli et muulla tavoin osaa päätellä tekijän merkkiä eri väleillä, voit aina tehdä sen kokeilemalla. Lopuksi päätellään derivaatan merkki eri väleillä tulon merkkisääntöä soveltaen. Tämän jälkeen merkitään kaavioon esimerkiksi nuolilla, onko funktio kyseisellä välillä aidosti kasvava vai aidosti vähenevä.
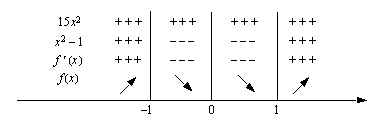
Derivaatan merkkikaavion perusteella funktio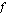 
on aidosti kasvava väleillä 
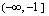ja 
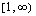sekä aidosti vähenevä välillä 
.
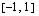Funktion kuvaajan piirtämiseksi lasketaan siltä muutama piste. Nyt, kun tiedämme funktion kulun pääpiirteissään, riittää, että laskemme funktion arvon derivaatan nollakohdissa sekä muutamassa muussa pisteessä.
ja 
(b) 
kuvaaja: 