Funktio on määrittelyjoukossaan derivoituva, joten sillä voi olla lokaali ääriarvo ainoastaan derivaatan nollakohdassa. Määrätään ensin funktion derivaatta:
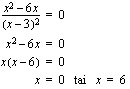
Laaditaan sitten derivaatan merkkikaavio. Koska funktio ei ole määritelty kohdassa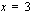 
, merkitään tämä kohta myös merkkikaavioon. Funktion kuvaajahan katkeaa kyseisessä kohdassa joka tapauksessa. Derivaatan merkin selvittämiseksi eri väleillä voidaan tutkia erikseen derivaatan osoittajan ja nimittäjän merkkejä ja päätellä sitten itse derivaatan merkki osamäärän merkkisääntöä soveltaen. Koska derivaatan nimittäjänä on neliö, joka on aina positiivinen, määrää derivaatan osoittaja suoraan myös koko derivaatan merkin. Tässä päätellään siis derivaatan merkki eri väleillä suoraan 
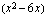:n merkistä. Lausekkeen 
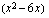kuvaaja on ylöspäin aukeava paraabeli, joten se saa negatiivisia arvoja nollakohtien välissä ja positiivisia arvoja niiden ulkopuolella. .
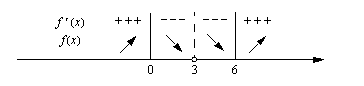
Funktiolla on siten lokaali maksimi kohdassa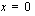 
. Kyseinen maksimiarvo on 
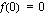. Funktiolla on puolestaan lokaali minimi kohdassa 
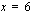. Kyseinen minimiarvo on 
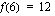. Huomaa, että maksimiarvo on pienempi kuin miniarvo. Tämä on mahdollista siksi, että funktiolla on epäjatkuvuuskohta näiden kohtien välissä. Funktion kuvaaja voidaan nyt piirtää, kun lasketaan siltä ensin muutama lisäpiste.
.
ja minimi 
. 
kuvaaja: 