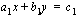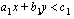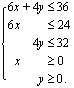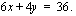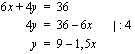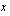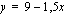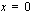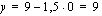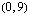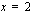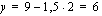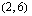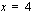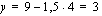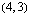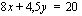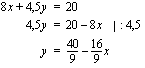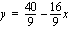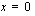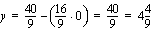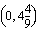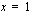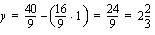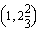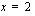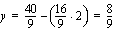[edellinen] [sisällys] [seuraava]
3.1. Lineaarinen optimointiongelma
3.1.1. Matemaattinen malli
Ratkaistiinpa lineaarinen optimointiongelma teknisesti millä menetelmällä tahansa, siitä on aina ensin muodostettava matemaattinen malli. Tarkastellaan tämän mallin muodostamista seuraavan yksinkertaisen esimerkkiongelman avulla.
Esimerkki 3.1.
Mäkelän emäntä hankkii joutoaikanaan lisätuloja kutomalla poppanoita sekä valmistamalla kangasväreillä käsin painettuja verhokappoja. Käsityöt hän käy tekemässä läheisellä kylätalolla, jossa on kangaspuita sekä kankaanpainantaan sopivat tilat. Emännältä liikenee käsitöihin aikaa 36 h/kk. Poppanaliinan kutomiseen häneltä kuluu 6 h/kpl ja verhon valmistukseen päärmimisineen 4 h/kpl. Poppanaliinan materiaalikustannukset ovat 8 euroa/kpl ja verhon 3,5 euroa/kpl. Käsityöt myydään paikallisessa suoramyyntipisteessä, missä taitavana tunnetun emännän työt menevät aina kaupaksi. Emäntä saa poppanaliinasta 16 euroa/kpl ja verhosta 8 euroa/kpl. Kylätalolla on tilojen suuren kysynnän vuoksi jouduttu asettamaan kangaspuiden maksimikäyttöajaksi 24 h/kk ja kankaanpainantaan sopivien tilojen käyttöajaksi 32 h/kk yhdeltä hengeltä.
Kuinka monta poppanaa ja kuinka monta verhokappaa Mäkelän emännän kannattaisi kuukaudessa näiden rajoitteiden puitteissa valmistaa, jotta hänen saamansa myyntivoitto olisi mahdollisimman suuri?
Tämän esimerkin ratkaisu esitetään myöhemmin luvussa 3.2.2. Sitä ennen ongelmasta muodostetetaan matemaattinen malli.
Kun lineaarisesta optimointiongelmasta muodostetaan matemaattinen malli, on selvitettävä seuraavat kolme asiaa:
- muuttujat, joiden arvo halutaan tietää tavoitellussa optimitilanteessa,
- tavoitefunktio, joka halutaan minimoida tai maksimoida sekä
- toimintaa rajoittavat ehdot, joiden on oltava voimassa löydetyssä ratkaisukohdassa.
Tarkastellaan matemaattisen mallin muodostamista edellä esitetyn esimerkin valossa. Sen ongelmana on selvittää, kuinka monta poppanaa ja verhokappaa Mäkelän emännän on kuukaudessa valmistettava, jotta hänen saamansa myyntivoitto olisi mahdollisimman suuri. Etsittyjä muuttujia ovat siis nuo käsitöiden määrät. Tässä on kyseessä kahden muttujan lineaarinen optimointiongelma. Kun lineaarisessa optimointiongelmassa on vain kaksi muuttujaa, niitä merkitään yleensä tunnuksin 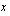 ja
ja 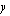 . Sovitaan esimerkiksi tässä tapauksessa, että Mäkelän emännän kuukaudessa valmistamien poppanoiden määrä on
. Sovitaan esimerkiksi tässä tapauksessa, että Mäkelän emännän kuukaudessa valmistamien poppanoiden määrä on 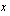 kpl/kk ja verhokappojen määrä
kpl/kk ja verhokappojen määrä 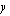 kpl/kk. Kun lineaarisessa optimointiongelmassa on useampia muuttujia (niitä voi olla vaikka satoja), niitä merkitään seuraavasti:
kpl/kk. Kun lineaarisessa optimointiongelmassa on useampia muuttujia (niitä voi olla vaikka satoja), niitä merkitään seuraavasti:
Etsiessäsi lineaarisen optimointiongelman muuttujia, sinun kannattaa siis miettiä, minkä suureiden arvoja halutussa optimitilanteessa haetaan. Muuttujat voivat olla esimerkiksi yrityksen eri tuotteiden tuotantonopeuksia tai tehtaan eri varastoihin sijoitettavien tuotteiden määriä.
Muutujien löytämisen jälkeen sinun on mietittävä, mitä suuretta optimointiongelmassa pyritään minimoimaan tai maksimoimaan. Edellisessä esimerkissä se oli Mäkelän emännän saama myyntivoitto. Ongelman matemaattista mallia varten muodostettava tavoitefunktio ilmoittaa, kuinka tuo optimoitava suure lasketaan edellä löydettyjen muuttujien avulla.
Esimerkki 3.1. jatkuu ...
Muodostetaan tavoitefunktio esimerkistä 3.1. Pyritään esittämään maksimoitava kuukausittainen myyntivoitto valittujen muuttujien 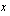 kpl/kk (poppanoiden määrä) ja
kpl/kk (poppanoiden määrä) ja 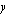 kpl/kk (verhokappojen lukumäärä) avulla. Myyntivoitto saadaan vähentämällä kuukauden myyntituloista käsitöiden valmistuksesta aiheutuneet kustannukset. Koska poppanan myyntihinta oli 16 euroa/kpl ja verhon myyntihinta 8 euroa/kpl, ovat käsitöiden myynnistä saadut tulot
kpl/kk (verhokappojen lukumäärä) avulla. Myyntivoitto saadaan vähentämällä kuukauden myyntituloista käsitöiden valmistuksesta aiheutuneet kustannukset. Koska poppanan myyntihinta oli 16 euroa/kpl ja verhon myyntihinta 8 euroa/kpl, ovat käsitöiden myynnistä saadut tulot
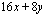 .
.
Valmistuskustanukset muodostuvat nyt pelkästään materiaalikustannuksista. Poppanan materiaalikustannukset olivat 8 euroa/kpl ja verhon 3,5 euroa/kpl. Tällöin valmistuskustannukset olivat yhteensä
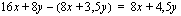 .
.
Esimerkkiongelmassa maksimoitava tavoitefunktio on käsitöiden myynnistä saatavaa kuukausittaista voittoa esittävä funktio
Lineaarisen optimointiongelman tavoitefunktio on aina lineaarinen funktio. Tämä tarkoittaa sitä, että funktio voidaan aina esittää summana, jonka yhteenlaskettavat ovat joko vakiolla kerrottuja muuttujia tai pelkkiä vakioita. Nämä vakiot voivat olla esimerkiksi reaalilukuja tai mittayksiköllisiä suureita. Jos kyseessä on kahden muuttujan 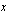 ja
ja 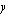 lineaarinen optimointiongelma, sen tavoitefunktio on aina muotoa
lineaarinen optimointiongelma, sen tavoitefunktio on aina muotoa
Vakio 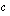 saa usein arvon nolla kuten kävi esimerkkitapauksessamme. Jos lineaarisessa optimointiongelmassa on
saa usein arvon nolla kuten kävi esimerkkitapauksessamme. Jos lineaarisessa optimointiongelmassa on 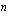 kpl muuttujia, jotka ovat
kpl muuttujia, jotka ovat 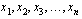 , niin sen tavoitefunktion on oltava muotoa
, niin sen tavoitefunktion on oltava muotoa
Viimeiseksi lineaarisen optimointiongelman matemaattista mallia muodostettaessa on mietittävä ne toimintaa rajoittavat ehdot (rajoitteet), joiden on oltava voimassa löydetyssä optimointiongelman ratkaisukohdassa. Ehdot esitetään ensimmäisen asteen yhtälöinä tai epäyhtälöinä (niissä ei esiinny muuttujien potensseja vaan termit ovat muuttujien lineaariyhdistelyjä). Jos lineaarisessa optimointiongelmassa on 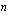 muuttujaa (
muuttujaa (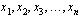 ), sen kaksi ensimmäistä rajoitetta ovat muotoa
), sen kaksi ensimmäistä rajoitetta ovat muotoa
missä muuttujien kertoimet 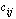 sekä epäyhtälöiden oikean puolen termit
sekä epäyhtälöiden oikean puolen termit 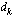 ovat vakioita. Näiden vakioiden indeksoinnin ensimmäinen luku kertoo aina, monennestako rajoitteesta on kysymys, ja toinen luku, minkä muuttujan kerroin vakio on. Rajoitteissa voi tietysti olla mika tahansa muu epäyhtälömerkki
ovat vakioita. Näiden vakioiden indeksoinnin ensimmäinen luku kertoo aina, monennestako rajoitteesta on kysymys, ja toinen luku, minkä muuttujan kerroin vakio on. Rajoitteissa voi tietysti olla mika tahansa muu epäyhtälömerkki  tai yhtäsuuruusmerkki (=).
tai yhtäsuuruusmerkki (=).
Rajoitteita toiminnalle aiheuttavat esimerkiksi rajalliset materiaali-, työntekijä- tai koneenkäyttökapasiteetit, tietyt toiminnan vähimmäisvaatimukset tai rajalliset tuotantokustannukset. Esimerkkiongelmassamme emännän käsitöiden tekoa rajoittivat käytettävissä oleva aika 36 h/kk, kangaspuiden rajoitettu käyttöaika 24 h/kk sekä kankaanpainantatilojen rajoitettu käyttöaika 32 h/kk. Muodostetaan seuraavaksi esimerkkiongelmamme rajoitteet valittujen muuttujien avulla.
Esimerkki 3.1. jatkuu ...
Koska emännältä kuluu poppanan kutomiseen 6 h/kpl ja verhon valmistukseen 4 h/kpl ja hänellä on aikaa käsitöiden valmistamiseen 36 h/kk, on kuukaudessa valmistettujen poppanoiden määrän 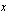 kpl/kk ja verhojen määrän
kpl/kk ja verhojen määrän 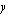 kpl/kk toteutettava epäyhtälö
kpl/kk toteutettava epäyhtälö
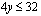 .
.
Lisäksi valmistettujen käsitöiden lukumäärät eivät voi olla negatiivisia, joten on oltava voimassa
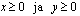 .
.
Esimerkkiongelmamme on nyt matematisoitu. Lyhyesti sanottuna ongelmana on löytää kuukausittain valmistettavien poppanoiden määrä 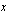 kpl/kk ja verhojen määrä
kpl/kk ja verhojen määrä 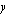 kpl/kk siten, että emännän käsitöidensä myynnistä saama kuukausittainen myyntivoitto
kpl/kk siten, että emännän käsitöidensä myynnistä saama kuukausittainen myyntivoitto
Ratkaistessasi mitä tahansa lineaarista optimointiongelmaa käsin tai taulukkolaskentaohjelmalla sinun on laadittava siitä edellä esitetyn kaltainen matemaattinen malli, josta ilmenee muuttujat, tavoitefunktio sekä muuttujien rajoitteet. Ennen kuin harjoittelemme lisää lineaaristen optimointiongelmien matematisointia, katsotaan vielä, kuinka tällainen ongelma voidaan havainnollistaa tasokoordinaatistossa kahden muuttujan tapauksessa.
3.1.2. Havainnollistaminen
Silloin kun lineaarisessa optimointiongelmassa on vain kaksi muuttujaa, se voidaan havainnollistaa geometrisesti tasokoordinaatistossa. Tarkastellaan aluksi rajoitteiden havainnollistamista. Kahden muuttujan optimointiongelmassa rajoitteet ovat muotoa
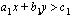 .
.
Kahden muuttujan lineaarisen optimointiongelman edellä kuvattua muotoa olevat rajoitteet muodostavat ns. lineaarisen epäyhtälöryhmän, jos kaikki rajoitteet ovat epäyhtälöitä. Tällöin kunkin epäyhtälön ratkaisujoukko on jokin tason suoran rajoittama alue. Epäyhtälöryhmän ratkaisun on toteutettava kaikki ryhmän epäyhtälöt. Kahden muuttujan lineaarisen optimointiongelman rajoitteet esittävät siten jotakin tason suorien rajoittamaa aluetta.
Palataan esimerkkiongelmaamme ja havainnollistetaan sen rajoitteet tason suorien rajoittamana alueena.
Esimerkki 3.1. jatkuu ...
Epäyhtälöryhmän havainnollistamiseksi on pystyttävä piirtämään kutakin epäyhtälöä vastaavan yhtälön kuvaajasuora sekä päättelemään, kummalla puolella suoraa kyseinen epäyhtälö toteutuu. Tarkastellaan ensin ensimmäistä epäyhtälöä vastaavaa yhtälöä
Tätä yhtälöä esittävän suoran piirtämiseksi on siltä määrättävä ainakin kaksi pistettä. Tämä tapahtuu antamalla toiselle koordinaatille (esim. 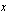 :lle) arvoja ja laskemalla yhtälön avulla vastaavat toisen koordinaatin (esim.
:lle) arvoja ja laskemalla yhtälön avulla vastaavat toisen koordinaatin (esim. 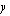 :n) arvot. Annetaan tässä
:n) arvot. Annetaan tässä 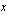 :lle arvot 0, 2 ja 4 sekä lasketaan vastaavat
:lle arvot 0, 2 ja 4 sekä lasketaan vastaavat 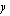 :n arvot. Ne saadaan kätevästi ratkaisemalla
:n arvot. Ne saadaan kätevästi ratkaisemalla 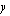 suoran yhtälöstä.
suoran yhtälöstä.
Kolmas piste on tässä varmistukseksi, että kaikki määrätyt pisteet ovat varmasti kyseisellä suoralla. Nyt suora voidaan piirtää sijoittamalla löydetyt pisteet koordinaatistoon ja piirtämällä suora kulkemaan niiden kautta. Suora on esitetty oheisessa kuviossa
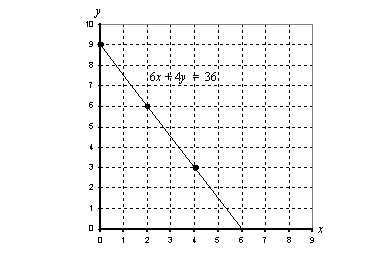
Lopuksi päätellään vielä, toteutuuko rajoite-epäyhtälö 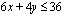 tämän suoran ylä- vai alapuolella. Sen voi selvittää helposti kokeilemalla. Valitaan esimerkiksi suoran alapuolelta yksi piste. Jos ehto toteutuu tässä pisteessä, epäyhtälö toteutuu suoran alapuolella, muussa tapauksessa se toteutuu suoran yläpuolella. Valitaan nyt kokeilupisteeksi
tämän suoran ylä- vai alapuolella. Sen voi selvittää helposti kokeilemalla. Valitaan esimerkiksi suoran alapuolelta yksi piste. Jos ehto toteutuu tässä pisteessä, epäyhtälö toteutuu suoran alapuolella, muussa tapauksessa se toteutuu suoran yläpuolella. Valitaan nyt kokeilupisteeksi 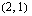 . Sijoitetaan
. Sijoitetaan 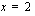 ja
ja 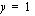 rajoite-epäyhtälön vasemmalle puolelle. Tulokseksi saadaan
rajoite-epäyhtälön vasemmalle puolelle. Tulokseksi saadaan
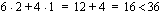 ,
,
joten epäyhtälön ehto toteutuu tässä pisteessä. Rajoite-epäyhtälö 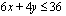 toteutuu siten suoralla
toteutuu siten suoralla 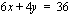 (yhtäsuuruus sisältyy ehtoon) ja sen alapuolella.
(yhtäsuuruus sisältyy ehtoon) ja sen alapuolella.
Tällä tavoin tutkitaan kaikki rajoite-epäyhtälöryhmän muut epäyhtälöt. Epäyhtälö 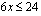 , joka voidaan myös esittää muodossa
, joka voidaan myös esittää muodossa 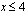 , toteutuu pystysuoralla suoralla
, toteutuu pystysuoralla suoralla 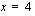 ja sen vasemmalla puolella. Epäyhtälö
ja sen vasemmalla puolella. Epäyhtälö 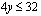 eli
eli 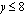 toteutuu vaakasuoralla suoralla
toteutuu vaakasuoralla suoralla 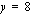 sekä sen alapuolella. Muuttujien positiivisuusehdot
sekä sen alapuolella. Muuttujien positiivisuusehdot 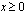 ja
ja 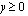 puolestaan toteutuvat positiivisilla koordinaattiakseleilla sekä koordinaatiston ensimmäisessä neljänneksessä, jossa molemmat koordinaatit ovat positiiviset. Piirretään nämä kaikki suorat samaan koordinaatistoon ja varjostetaan näiden suorien rajoittamista alueista se, jossa kaikki esimerkkiongelman rajoite-epäyhtälöt toteutuvat. Tulos on esitetty seuraavassa kuviossa.
puolestaan toteutuvat positiivisilla koordinaattiakseleilla sekä koordinaatiston ensimmäisessä neljänneksessä, jossa molemmat koordinaatit ovat positiiviset. Piirretään nämä kaikki suorat samaan koordinaatistoon ja varjostetaan näiden suorien rajoittamista alueista se, jossa kaikki esimerkkiongelman rajoite-epäyhtälöt toteutuvat. Tulos on esitetty seuraavassa kuviossa.
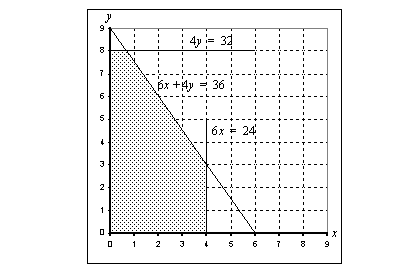
Esimerkkinä käyttämämme lineaarinen optimointiongelma voidaan tulkita geometrisesti siten, että on löydettävä edellä esitetystä rajoite-ehdot toteuttavasta monikulmiosta se korrdinaatiston piste 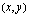 , jossa tavoitefunktio
, jossa tavoitefunktio 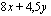 saa suurimman arvonsa. Yleisesti lineaarisessa optimointitehtävässä haetaan rajoitteet toteuttavasta tasoalueesta se piste, jossa lineaarinen tavoitefunktio saa suurimman tai pienimmän arvonsa. Kun tarkasteltava alue on tason monikulmio ratkaisu löytyy aina jostakin monikulmion kärkipisteestä tai kaksi kärkeä yhdistävältä janalta. Perustellaan tämä väite käyttäen tarkastelussa apuna esimerkkiongelmaamme.
saa suurimman arvonsa. Yleisesti lineaarisessa optimointitehtävässä haetaan rajoitteet toteuttavasta tasoalueesta se piste, jossa lineaarinen tavoitefunktio saa suurimman tai pienimmän arvonsa. Kun tarkasteltava alue on tason monikulmio ratkaisu löytyy aina jostakin monikulmion kärkipisteestä tai kaksi kärkeä yhdistävältä janalta. Perustellaan tämä väite käyttäen tarkastelussa apuna esimerkkiongelmaamme.
Esimerkkimme tavoitefunktio, joka esittää emännän käsitöiden myynnistä saamaa kuukausittaista myyntivoittoa, on
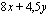 ,
,
missä 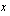 on kuukaudessa valmistettujen poppanoiden lukumäärä ja
on kuukaudessa valmistettujen poppanoiden lukumäärä ja 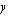 verhokappojen lukumäärä. Annetaan tälle tavoitefunktiolle (eli kuukausittaiselle myyntivoitolle) eri arvoja ja piirretään näitä yhtälöitä vastaavat suorat samaan koordinaatistoon rajoitemonikulmion kanssa. Annetaan tavoitefunktiolle esimerkiksi arvot 20, 30 ja 40. Yhtälön
verhokappojen lukumäärä. Annetaan tälle tavoitefunktiolle (eli kuukausittaiselle myyntivoitolle) eri arvoja ja piirretään näitä yhtälöitä vastaavat suorat samaan koordinaatistoon rajoitemonikulmion kanssa. Annetaan tavoitefunktiolle esimerkiksi arvot 20, 30 ja 40. Yhtälön
kuvaaja on suora, jonka piirtämiseksi meidän on ensin määrättävä siltä muutama piste. Tämän suoran pisteitä vastaavilla käsitöiden määrillä emännän saama kuukausittainen voitto on 20 euroa/kk. Ratkaistaan suoran piirtämistä varten muuttuja 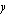 sen yhtälöstä.
sen yhtälöstä.
Määrätään suoralta kolme pistettä.
Vastaavalla tavalla havaitaan, että yhtälön 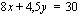 kuvaajasuora kulkee pisteiden
kuvaajasuora kulkee pisteiden 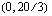 ,
, 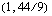 ja
ja 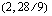 kautta. Tämän suoran pisteitä vastaavilla poppana- ja verhomäärillä emännän saama kuukausittainen myyntivoitto on 30 euroa. Käsitöiden kuukausittainen myyntivoitto on 40 euroa yhtälön
kautta. Tämän suoran pisteitä vastaavilla poppana- ja verhomäärillä emännän saama kuukausittainen myyntivoitto on 30 euroa. Käsitöiden kuukausittainen myyntivoitto on 40 euroa yhtälön 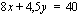 ratkaisupisteissä, joita ovat esimerkiksi
ratkaisupisteissä, joita ovat esimerkiksi 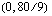 ,
, 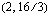 ja
ja  . Oheiseen kuvioon on piirretty nämä tavoitefunktion arvoja 20, 30 ja 40 vastaavat suorat sekä rajoitemonikulmio.
. Oheiseen kuvioon on piirretty nämä tavoitefunktion arvoja 20, 30 ja 40 vastaavat suorat sekä rajoitemonikulmio.
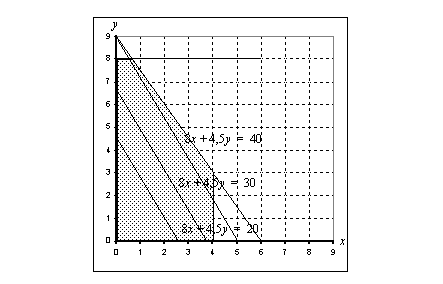
Kuviosta havaitaan, että eri kuukausittaisia myyntivoittoja esittävät suorat muodostavat keskenään yhdensuuntaisten suorien parven. Mitä suurempi on emännän saama kuukausittainen myyntivoitto, sitä korkeammalla kysenen suora on kuviossa. Se poppanoiden ja verhokappojen kuukausittainen valmistusmäärä, jolla emännän saama myyntivoitto on mahdollisimman suuri löytyy etsimällä eri myyntivoittoja kuvaavasta suoraparvesta se, joka on mahdollisimman ylhäällä ja sisältää vielä rajoitemonikulmion pisteitä. Esimerkkimme optimointiongelman voikin ratkaista graafisesti siirtämällä myyntivoittoa esittävää suoraa ylöspäin suuntansa säilyttäen, kunnes löytyy mahdollisimman ylhäällä oleva suora, joka vielä sisältää ongelman rajoitemonikulmion pisteen/pisteitä.
Kahden muuttujan lineaarisen optimointiongelman tavoitefunktio saa eri arvonsa suorilla, jotka ovat toisensa kanssa yhdensuuntaiset. Tällaisen lineaarisen optimointiongelman voi aina ratkaista graafisesti siirtämällä yhtä tavoitefunktion arvoa esittävää suoraa suuntansa säilyttäen niin, että löytyy mahdollisimman ylhäällä tai alhaalla oleva suora (riipuen siitä, onko kyseessä minimointi- vai maksimointiongelma), joka vielä sisältää rajoite-epäyhtälöryhmän toteuttavan alueen pisteitä. Jos rajoite-epäöyhtälöryhmää esittää tasomonikulmio, on ratkaisuna aina joko yksi monikulmion kärkipiste tai kaksi kärkeä yhdistävä jana.
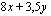 .
.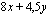 .
.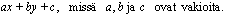

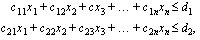
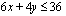 .
.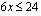
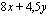
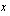 ja
ja 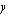 rajoittavat ehdot
rajoittavat ehdot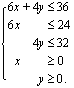
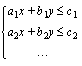
 tai rajoite voi olla yhtälö. Yhtälön
tai rajoite voi olla yhtälö. Yhtälön