[edellinen] [sisällys] [seuraava]
3.2. Lineaarisen optimointiongelman ratkaiseminen
3.2.1. Ratkaisutapoja
Kun lineaarisessa optimointiongelmassa on vain kaksi muuttujaa, sen voi ratkaista helposti myös käsin. Edellä kuvattiin jo graafista ratkaisutapaa. Tällöin piirretään ensin rajoite-epäyhtälöryhmän ratkaisualue (yleensä monikulmio) tasokoordinaatistoon. Lineaarinen tavoitefunktio saa nyt eri arvonsa suorilla, jotka ovat keskenään yhdensuuntaiset. Optimointiongelma ratkeaa, kun löydetään näistä yhdensuuntaisista suorista se, jolla tavoitefunktion arvo on mahdollisimman suuri (maksimointiongelma) tai mahdollisimman pieni (minimointiongelma) ja joka vielä sisältää rajoitealueen pisteitä. Tämä etsintä voidaan tehdä piirtämällä yhtä tavoitefunktion arvoa vastaava suora ja siirtämällä sitä suuntansa säilyttäen ylös- tai alaspäin, kunnes ratkaisupiste saavutetaan. Kun rajoitealue on tasomonikulmio, ratkaisu on monikulmion kärkipisteessä tai kaksi kärkeä yhdistävällä janalla.
Silloin, kun rajoitealue on monikulmio, kahden muuttujan lineaarisen optimointiongelman ratkaisun voi löytää helposti myös laskemalla. Tiedetään, että ratkaisu on tällöin jossakin monikulmion kärkipisteessä tai kahden kärjen välisellä janalla. Koska tasomonikulmion kärjet ovat suorien leikkauspisteitä, ne voi ratkaista näiden suorien yhtälöiden muodostaman yhtälöparin avulla. Kun kaikki rajoitemonikulmion kärjet on ratkaistu, lasketaan tavoitefunktion arvo kussakin niistä. Arvoista etsitään suurin tai pienin ongelmasta riippuen. Jos tavoitefunktio saa suurimman tai pienimmän arvonsa kahdessa eri pisteessä, ovat näitä kärkipisteitä yhdistävän janan kaikki pisteet ratkaisukohtia.
Kun lineaarisessa optimointiongelmassa on muuttujia enemmän kuin kaksi, se kannattaa ratkaista tietokoneen avulla. Lineaaristen optimointiongelmien ratkaisemiseksi on kehitelty erilaisia laskentamenetelmiä, kuten simplex-algoritmi. Tällä kurssilla näitä menetelmiä ei kuitenkaan esitellä tarkemmin.
3.2.2. Ratkaiseminen laskemalla
Kahden muuttujan lineaarinen optimointiongelma, jonka rajoitealue on monikulmio, ratkeaa helposti myös käsin laskemalla. Kuten edellä on perustellen todettu, ratkaisu on tässä tapauksessa joko jossakin monikulmion kärkipisteessä tai kaksi kärkeä yhdistävällä janalla. Ratkaisu löydetään tällöin laskemalla ensin rajoitemonikulmion kaikki kärkipisteet esimerkiksi yhtälöparien avulla ja laskemalla sitten tavoitefunktion arvo näissä pisteissä. Sen mukaan, onko kyseessä minimointi- vai maksimointiongelma, ratkaisu löytyy joko tavoitefunktion pienimmän tai suurimman arvon avulla. Ratkaistaan nyt esimerkkiongelmamme laskemalla.
Esimerkki 3.1. ratkaisutapa I
Mäkelän emäntä hankkii joutoaikanaan lisätuloja kutomalla poppanoita sekä valmistamalla kangasväreillä käsin painettuja verhokappoja. Käsityöt hän käy tekemässä läheisellä kylätalolla, jossa on kangaspuita sekä kankaanpainantaan sopivat tilat. Emännältä liikenee käsitöihin aikaa 36 h/kk. Poppanaliinan kutomiseen häneltä kuluu 6 h/kpl ja verhon valmistukseen päärmimisineen 4 h/kpl. Poppanaliinan materiaalikustannukset ovat 8 euroa/kpl ja verhon 3,5 euroa/kpl. Käsityöt myydään paikallisessa suoramyyntipisteessä, missä taitavana tunnetun emännän työt menevät aina kaupaksi. Emäntä saa poppanaliinasta 16 euroa/kpl ja verhosta 8 euroa/kpl. Kylätalolla on tilojen suuren kysynnän vuoksi jouduttu asettamaan kangaspuiden maksimikäyttöajaksi 24 h/kk ja kankaanpainantaan sopivien tilojen käyttöajaksi 32 h/kk yhdeltä hengeltä.
Kuinka monta poppanaa ja kuinka monta verhokappaa Mäkelän emännän kannattaisi kuukaudessa näiden rajoitteiden puitteissa valmistaa, jotta hänen saamansa myyntivoitto olisi mahdollisimman suuri?
Muodostettuamme edellä matemaattisen mallin tästä ongelmasta totesimme, että tavoitteena on löytää kuukausittain valmistettavien poppanoiden määrä 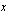 kpl/kk ja verhojen määrä
kpl/kk ja verhojen määrä 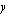 kpl/kk siten, että emännän käsitöidensä myynnistä saama kuukausittainen myyntivoitto
kpl/kk siten, että emännän käsitöidensä myynnistä saama kuukausittainen myyntivoitto
Nämä rajoitteet toteutuvat oheiseen kuvioon varjostetussa monikulmiossa.
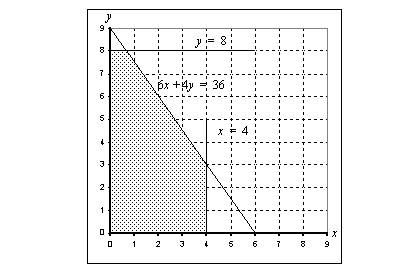
Koska tiedetään, että tämän optimointiongelman ratkaisukohta on jokin oheisen monikulmion kärkipiste tai kaksi kärkeä yhdistävä jana, on meidän selvitettävä aluksi nuo kärkipisteet. Monikulmion kärkipisteet  ,
, 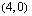 ja
ja 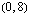 ilmenevät kuvion yhtälöistä suoraan ilman laskemista. Kaksi muuta kärkipistettä voidaan ratkaista yhtälöparien avulla.
ilmenevät kuvion yhtälöistä suoraan ilman laskemista. Kaksi muuta kärkipistettä voidaan ratkaista yhtälöparien avulla.
3.2.3. Ratkaiseminen Excelillä
Excel-taulukkolaskentaohjelman työkalut sisältää ratkaisimen (engl. versiossa solver), jonka avulla voi etsiä annetulle tavoitefunktiolle suurimman tai pienimmän arvon tiettyjen reunaehtojen voimassaollessa. Ratkaisin laskee samalla myös ne muuttujien arvot, joilla tämä suurin tai pienin arvo saavutetaan. Harjoitellaan lineaarisen optimointiongelman ratkaisemista tällä ratkaisimella esimerkkiongelmamme avulla.
Esimerkki 3.1. ratkaisutapa II
Mäkelän emäntä hankkii joutoaikanaan lisätuloja kutomalla poppanoita sekä valmistamalla kangasväreillä käsin painettuja verhokappoja. Käsityöt hän käy tekemässä läheisellä kylätalolla, jossa on kangaspuita sekä kankaanpainantaan sopivat tilat. Emännältä liikenee käsitöihin aikaa 36 h/kk. Poppanaliinan kutomiseen häneltä kuluu 6 h/kpl ja verhon valmistukseen päärmimisineen 4 h/kpl. Poppanaliinan materiaalikustannukset ovat 8 euroa/kpl ja verhon 3,5 euroa/kpl. Käsityöt myydään paikallisessa suoramyyntipisteessä, missä taitavana tunnetun emännän työt menevät aina kaupaksi. Emäntä saa poppanaliinasta 16 euroa/kpl ja verhosta 8 euroa/kpl. Kylätalolla on tilojen suuren kysynnän vuoksi jouduttu asettamaan kangaspuiden maksimikäyttöajaksi 24 h/kk ja kankaanpainantaan sopivien tilojen käyttöajaksi 32 h/kk yhdeltä hengeltä.
Kuinka monta poppanaa ja kuinka monta verhokappaa Mäkelän emännän kannattaisi kuukaudessa näiden rajoitteiden puitteissa valmistaa, jotta hänen saamansa myyntivoitto olisi mahdollisimman suuri?
Laaditaan taulukko, josta ilmenevät etsityt muuttujat (kuukaudessa valmistettavien poppanoiden ja verhokappojen määrät), tavoitefunktio (kuukausittainen myyntivoitto) sekä rajoitteet. Esimerkissämme rajoitteet liittyivät aikaan. Oheisessa taulukossa on esitetty tehtävän reunaehtojen ratkaisimeen kirjoittamista varten sekä aikarajoitteiden kokonaiskapasiteetit että näiden kapasiteettien käyttö tietyillä poppana- ja verhomäärillä. Kaava(t)-sarakkeista ilmenee viereisen sarakkeen suureen arvon laskemiseen käytetty kaava.
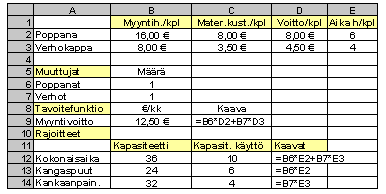
Tavoitteenamme on löytää sellaiset käsitöiden lukumäärät, joilla myyntivoittofunktio on mahdollisimman suuri, kun käsitöiden valmistukseen käytetty kokonaisaika, kangaspuiden ja kankaanpainantatilojen käyttöaika on korkeintaan ilmoitetun kapasiteetin suuruinen.
Optimointitehtävän ratkaisemiseksi valitaan Excelin työkaluista ratkaisin. Tämän jälkeen annetaan ratkaisimen vaatimat parametrit seuraavan luettelon ja oheisen kuvion mukaisesti.
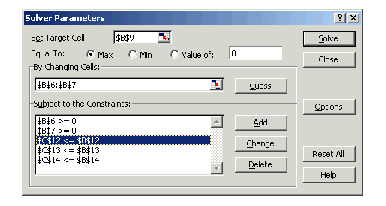
- Määrätään solu (Target Cell), jonka arvo halutaan minimoida tai maksimoida. Tässä kohtaan annetaan solu $B$9, johon on laskettu tavoitefunktion eli myyntivoittofunktion arvo.
- Ilmoitetaan, halutaanko solun arvo minimoida vai maksimoida. (Ratkaisimen avulla voi myös selvittää, millä muuttujan arvolla tavoitefunktio saa tietyn arvon. Tätä toimintoa emme nyt käytä.)
- Muuttamalla soluja -kohtaan (By Changing Cells) annetaan muuttujat sisältävien solujen osoitteet. Tässä ne ovat käsitöiden määrät ilmoittavat solut eli $B$6:$B$7. Muuttujille annetaan aluksi jotkut sopivat arvot (esimerkiksi 0 tai 1).
- Lisätään (Add) optimointiongelman rajoitteet reunaehdot-kohtaan (Constraints). Kukin reunaehto sisältää soluviittauksen solusta, jonka arvoa ehto koskee, reunaehdon epäyhtälömerkin (tai yhtäsuuruusmerkin) sekä soluviittauksen, joka ilmaisee kyseisen reunaehdon epäyhtälön (tai yhtälön) toisen puolen arvon. Tässä tapauksessa reunaehdot ovat $C$12 <= $B$12, $C$13 <= $B$13 ja $C$14 <= $B$14 sekä lisäksi positiivisuusehdot $B$6 >= 0 ja $B$7 >= 0.
Ratkaise-painikkeella (Solve) aloitetaan ratkaisun hakeminen, kun kaikki parametrit on annettu. Ratkaisin ilmoittaa, löysikö se ratkaisun. Valitsemalla ratkaisimen tuloksista vaihtoehdon `käytä ratkaisimen arvoja', muuttujien arvot muuttuvat taulukossa optimitilannetta vastaaviksi. Valitsemalla vielä tarjotuista raporttivaihtoehdoista vastauksen (Answer), saa omalle arkille vastausraportin,
joka on esitettu oheisessa kuviossa englanninkielisen version antamana.
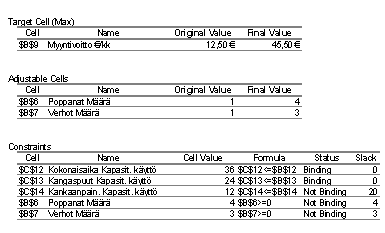
Vastausraportista ilmenee tavoitefunktion ja muuttujien arvot sekä alkutilanteessa että löydetyssä optimitilanteessa. Raportin reunaehdot-osiosta ilmenee reunaehdon kaava, reunaehdon solun arvo, joka esimerkkitilanteessamme kertoo kyseisen kapasiteetin käytön optimitilanteessa, sekä se, onko kyseinen resurssi optimitilanteessa kokonaan käytössä vai jääkö vapaata resurssia. Esimerkkimme optimitilanteessa, jossa valmistetaan kuukaudessa 4 poppanaa ja 3 verhokappaa ja saadaan myyntivoitoksi 45,5 euroa/kk, jää kankaanpainantatilojen käyttöajassa vapaata resurssia 20 h/kk, mutta muut resurssit ovat kokonaan käytössä.
Kun ratkaiset lineaarista optimointiongelmaa Excel-taulukkolaskentaohjelmalla, laadi taulukko, jossa on omat solut muuttujien sekä tavoitefunktion arvoja varten, sekä anna muuttujille sopivat alkuarvot. Reunaehtojen antamista varten lisää taulukkoon vielä solut, joista ilmenee kunkin rajoitteen sisältämän resurssin käyttö sekä kyseisen resurssin maksimi- tai minimiarvo.
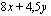
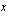 ja
ja 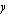 rajoittavat ehdot
rajoittavat ehdot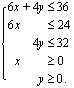
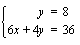
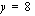 alempaan yhtälöön.
alempaan yhtälöön.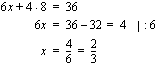
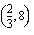 . Määrätään viimeinen puuttuva kärki samalla tavalla.
. Määrätään viimeinen puuttuva kärki samalla tavalla. 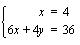
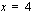 alempaan yhtälöön.
alempaan yhtälöön. 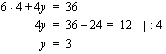
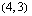 .
. 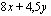 arvo näissä kärkipisteissä.
arvo näissä kärkipisteissä. 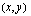
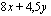
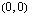
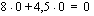
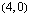
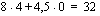
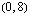
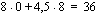
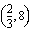
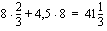
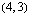
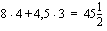
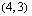 .
.