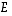1. Joukko-opin merkintöjä

Tässä ensimmäisessä luvussa esitämme muutamia tuttuja joukko-opin perusasioita, lähinnä nimityksien ja merkintätapojen kertauksen vuoksi.

Yleensä tässä kirjassa tarkasteltavat joukot tulevat olemaan jonkin tunnetun perusjoukon 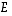osajoukkoja. Ne ilmoitetaan silloin muodossa

,

jossa lisämääreellä rajataan se, mitkä alkiot mukaan otetaan. Joukko voidaan ilmoittaa myös luettelemalla sen alkiot, esimerkiksi 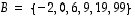. Tuttuja (perus)joukkoja ovat muun muassa

= luonnolliset luvut,

= kokonaisluvut,

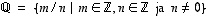= rationaaliluvut eli murtoluvut, ja

= reaaliluvut.

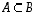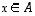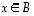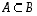Joukkojen sisältyvyys (, ) määritellään seuraavasti: , jos ehdosta seuraa aina, että . Kun , niin 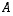on joukon 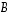osajoukko. Joukot ovat yhtäsuuret eli samat, 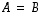, jos sek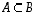ä että 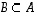. Huomaa, että sisältyvyys ei kiellä sitä mahdollisuutta, että joukot jo olisivat samoja, eli sisältyvyyden ei tarvitse olla aitoa.

Kahdelle perusjoukon 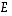osajoukolle 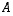ja 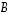voidaan muodostaa

yhdiste    ,

leikkaus     ja

erotus    .

Korkeintaan kolmesta joukosta näillä operaatioilla saatavat uudet joukot voidaan yleisesti kuvata ns. Vennin kuvioilla. Näillä Vennin kuvioilla voidaan myös selvittää, milloin erimuotoiset lausekkeet määrittelevät saman osajoukon. Voidaan esimerkiksi selvittää, ovatko joukot 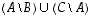ja 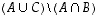aina samat eli päteekö yhtäsuuruus .

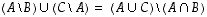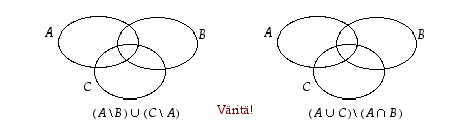
Jos valituksi tulevat täsmälleen samat kuvioiden palat, lausekkeiden määräämät joukotkin ovat aina samat. Väritä yllä oleviin kuvioihin kyseisiin joukkoihin kuuluvat palat ja totea, että samat palat tulevat väritettyä. Tämän mukaan esimerkkilausekkeet antavat aina samat joukot.

Joukoista voidaan muodostaa myös tulojoukkoja (eli karteesisia tuloja)

,

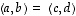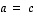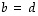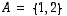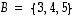missä esiintyville järjestetyille pareille sovitaan, että täsmälleen silloin, kun ja . Esimerkiksi joukoille ja on

.

Jos tulojoukossa 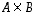tekijäjoukot ovat samat eli erikoisesti 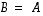, merkitään myös 'potenssimaisesti', että .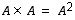

Tulojoukko yleistyy useammallekin tulon tekijälle, esimerkiksi

,

,

jne. Näissä esiintyvien kolmikkojen, nelikköjen jne. yhtäsuuruudet määritellään kuten pareille, ts. ensimmäisten alkioiden on oltava keskenään samat, toisten keskenään samat jne. Esimerkiksi 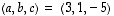vain silloin, kun 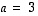, 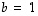ja .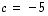

Jatkossa tarkastellaan erityisesti reaalilukujen tulojoukkoja

= taso,

= avaruus,

ja näiden yleistyksiä, ns. 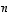- ulotteisia avaruuksia

,

missä 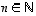, 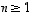. Tapauksessa 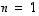kyseessä on ääritapaus, suora 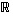, jonka alkiot ovat pelkkiä lukuja. Avaruuksia 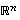sanotaan kreikkalaisen matemaatikon Eukleideen mukaan myös euklidisiksi avaruuksiksi. Niiden alkiot ovat siis 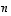luvusta muodostuvia (järjestettyjä) lukujonoja, 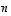- jonoja tai "ännikköjä". Tällaisen jonon lukuja sanotaan sen jäseniksi eli komponenteiksi.