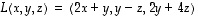Tehtävän 43 ratkaisu

Lasketaan kaikki lineaarikuvauksen 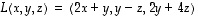ominaisarvot. Tätä lineaarikuvasta vastaava matriisi on

.

Kaikki lineaarikuvauksen ominaisarvot 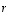saadaan yhtälön 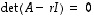ratkaisuina. Nyt

Asettamalla

,

saadaan

tai ,

eli tai

,

mistä saadaan, että

tai .

Ominaisarvot ovat siis ja .

Selvitetään vielä kaikki ominaisarvoa 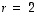vastaavat ominaisvektorit. Koska 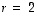on ominaisarvo, pätee yhtälö

kaikille ominaisvektoreille 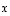. Tästä saadaan yhtälö

,

joka voidaan ratkaista Gauss-Jordanin menetelmällä. Aluksi saadaan matriisi

.

Lisätään ensin keskimmäinen rivi kaksi kertaa alimpaan riviin, lisätään sitten ylin rivi keskimmäiseen riviin ja vaihdetaan lopuksi keskimmäisen rivin merkit:

,

siis ominaisarvoa 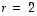vastaavat ominaisvektorit ovat kaikki muotoa 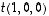olevat vektorit, missä 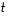on reaaliluku.

[Opiskelutehtävä 43][Vinkki tehtävään 43]