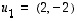 ja
ja 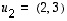 .
Vektoreita on kaksi kappaletta ja ne ovat lineaarisesti riippumattomat, joten ne käyvät kannaksi. Koska
.
Vektoreita on kaksi kappaletta ja ne ovat lineaarisesti riippumattomat, joten ne käyvät kannaksi. Koska 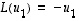 ja
ja 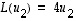 ,
voidaan suoraan vastata, että tässä kannassa lineaarikuvausta
,
voidaan suoraan vastata, että tässä kannassa lineaarikuvausta
Ominaisvektorit olivat siis 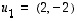 ja
ja 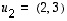 .
Vektoreita on kaksi kappaletta ja ne ovat lineaarisesti riippumattomat, joten ne käyvät kannaksi. Koska
.
Vektoreita on kaksi kappaletta ja ne ovat lineaarisesti riippumattomat, joten ne käyvät kannaksi. Koska 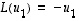 ja
ja 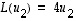 ,
voidaan suoraan vastata, että tässä kannassa lineaarikuvausta
,
voidaan suoraan vastata, että tässä kannassa lineaarikuvausta
vastaa ominaisarvojen muodostama diagonaalimatriisi
Tehdään sama myös laskemalla, eli tekemällä todella kannanvaihto kyseiseen kantaan. Kannanvaihtomatriisi on
Lisäksi lineaarikuvausta 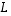 luonnollisessa kannassa vastaa matriisi
luonnollisessa kannassa vastaa matriisi
Täten lineaarikuvausta 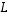 vastaa kannassa
vastaa kannassa 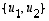 matriisi
matriisi
Tuloksena on ominaisarvojen muodostama diagonaalimatriisi kuten pitikin.
[Opiskelutehtävä 42][Vinkki tehtävään 42]