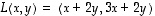Tehtävän 41 ratkaisu

Lineaarikuvausta 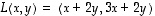vastaa matriisi

.

Jos vektori on ominaisvektori, on sille 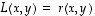jollekin reaaliluvulle 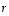. Nyt

,

joten 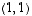ei ainakaan ole ominaisvektori. Samoin

,

joten myöskään 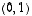ei ole ominaisvektori. Sen sijaan

,

eli 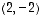on ominaisvektori, ominaisarvolla 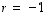. Vektorille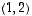

,

joten 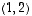ei ole ominaisvektori. Vektorille 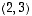taasen

eli 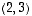on ominaisvektori ominaisarvolla 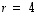. Viimeiselle vektorille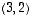

,

toisin sanoen 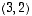ei ole ominaisvektori. Ominaisvektoreita olivat siis vain vektorit 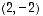ja 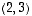ominaisarvoinaan 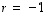ja .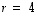

[Opiskelutehtävä 41][Vinkki tehtävään 41]