Tehtävän 36 ratkaisu

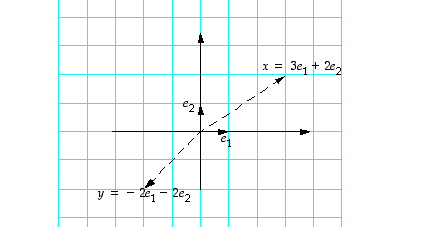
Geometrinen ratkaisu: Standardikannassa tilanne näyttää tältä:

Kannanvaihdon jälkeen tilanne näyttää tältä:

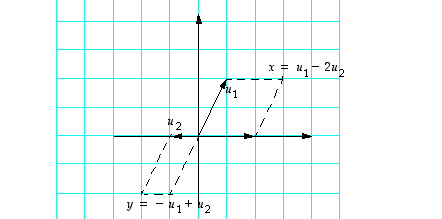
Pisteet 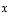ja 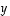pysyvät tietysti paikoillaan, mutta nyt niiden koordinaatit pitää lukea uudessa kannassa. Kuvaa katsomalla selviää, että uudessa kanssa pisteet ovat 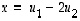ja .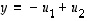

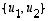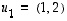Tehdään sama laskemalla kannanvaihtomatriisin avulla: Uusi kanta on , missä ja 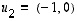. Täten kannanvaihtokuvausta vastaava matriisi tason luonnollisessa kannassa on

.

Voidaan osoittaa (esimerkiksi Gauss-Jordanin menetelmällä tai tehtävän 25 tavalla tai kokeilemalla) että matriisin 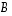käänteismatriisi on

.

Vektorin 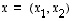koordinaatit 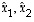kannassa 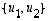saadaan kaavasta 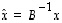. Täten vektorille on

,

siis

,

ja vastaavasti vektorille 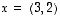on

,

siis

.

[Opiskelutehtävä 36][Vinkki tehtävään 36]