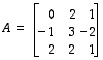 ,
,
Tutustumme nyt erääseen yhtälöryhmien algoritmiseen ratkaisumenetelmään. Tällä menetelmällä voidaan ratkaista lineaarisia yhtälöryhmiä hyvin systemaattisesti.
Tehdään edellä oleva eliminointiesimerkki seuraavassa yrittäen vapautua muuttujien kuljettamisesta koko ajan mukana. Katsotaankin vain kertoimien muuttumista ja pyritään pysyttelemään kertoimista muodostetuissa taulukoissa, joissa lukujen paikoista voidaan päätellä se, mihin muuttujaan ne liittyvät.
Muodostetaan yhtälöryhmän muuttujien kertoimista ensin lukutaulukko, ns. kerroinmatriisi
jonka (vaaka)
rivit muodostuvat muuttujien kertoimista yhtälöittäin annetussa järjestyksessä ja pystyrivit eli
sarakkeet muodostuvat vastaavasti saman muuttujan kertoimista eri yhtälöissä. Lisätään saatuun taulukkoon sitten yhtälöiden oikeitten puolien vakioluvut yhdeksi sarakkeeksi (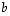 ). Näin muodostuu ns.
laajennettu
kerroinmatriisi
). Näin muodostuu ns.
laajennettu
kerroinmatriisi
Pystyviivalla (joka tässä on painoteknisistä syistä katkonainen) erotetaan yleensä kerroinosa (matriisi) ja vakio-osa (pystyvektori). Saatua laajennettua matriisia muokkaamme edellä kuvattua ratkaisumenettelyä seuraten. Päivitämme siis kerroinmatriisia sen mukaiseksi kuin se uusien yhtälöiden jälkeen on muokkautunut.
Vaihdetaan aluksi sen kaksi ensimmäistä riviä keskenään siinä tarkoituksessa, että 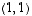 -paikkaan (eli ensimmäisen rivin ensimmäiseksi luvuksi) tulisi nollasta eroava luku. Kerrotaan samalla uusi ensimmäinen rivi luvulla
-paikkaan (eli ensimmäisen rivin ensimmäiseksi luvuksi) tulisi nollasta eroava luku. Kerrotaan samalla uusi ensimmäinen rivi luvulla 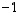 .
Silloin saadaan uusi (laajennettu) kerroinmatriisi
.
Silloin saadaan uusi (laajennettu) kerroinmatriisi
Edellä tehty operaatio vastaa alkuperäisessä yhtälöryhmässä kahden ensimmäisen yhtälön vaihtoa ja (alkuperäisen) toisen yhtälön merkin muutosta.
Vähennetään sitten ensimmäisen rivin luvut (luku luvulta edeten) kaksinkertaisena vastaavista kolmannen rivin luvuista. Päämääränä on tässä se, että kolmannen rivin ensimmäiseksi luvuksi tulee nolla. Saadaan kerrointaulukko
Yhtälöryhmän ratkaisussa tämä vaihe vastaa sitä, kun muuttuja 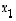 ratkaistiin muiden muuttujien avulla ja sijoitettiin kolmanteen yhtälöön (jolloin saatiin yhtälö (4) sen tilalle).
ratkaistiin muiden muuttujien avulla ja sijoitettiin kolmanteen yhtälöön (jolloin saatiin yhtälö (4) sen tilalle).
Nyt kerroinmatriisin ensimmäinen sarake on sellaista muotoa, johon yleisesti menetelmässä pyritään - ensimmäinen luku on ykkönen ja sen alla olevat ovat nollia. Sellaisena pyritään se pitämään jatkossakin.
Kerroinmatriisissa paikan 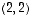 luku on nyt nollasta eroava (jos ei olisi ollut, olisi pyritty saamaan sellainen tilanne aikaan vaihtamalla toinen rivi jonkin alemman rivin kanssa). Vähennetään sitten toinen rivi (taaskin luku luvulta edeten) nelinkertaisena kolmannesta rivistä, jotta sen toinen luku muuttuisi nollaksi. Saadaan taulukko
luku on nyt nollasta eroava (jos ei olisi ollut, olisi pyritty saamaan sellainen tilanne aikaan vaihtamalla toinen rivi jonkin alemman rivin kanssa). Vähennetään sitten toinen rivi (taaskin luku luvulta edeten) nelinkertaisena kolmannesta rivistä, jotta sen toinen luku muuttuisi nollaksi. Saadaan taulukko
Tämä vaihe vastaa aikaisemmassa ratkaisussa muuttujan 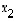 ratkaisemista ja sijoittamista yhtälöön (4).
ratkaisemista ja sijoittamista yhtälöön (4).
Jaetaan vielä saadun kerroinmatriisin toinen ja kolmas rivi niin, että lävistäjälle (vasemmasta yläkulmasta oikeaan alakulmaan) tulee vain ykkösiä:
Tämä teko vastaa yhtälöryhmissä vain yhtälöiden jakamista nollasta eroavilla luvuilla.
Nyt ns. menoalgoritmi on valmis. Sen jälkeen vasemman puolen neliömatriisissa pitäisi ihannetilanteessa olla lävistäjällä ykköset ja sen alapuolella nollat. Tähän ei tosin aina päästä. Näitä 'epäideaalisia' tilanteita käsitellään algoritmin esittelyn jälkeen.
Pyritään menoalgoritmin onnistumisen jälkeen seuraavaksi 'nollaamaan' myös lävistäjän yläpuoli. Kun menoalgoritmissa edettiin ylhäältä alas ja oikealle, edetään nyt vuorostaan alhaalta ylös ja vasemmalle.
Ensinnäkin kolmannen rivin avulla saadaan analogisesti aikaisemman menettelyn kanssa muokattua kolmannelle sarakkeelle yläpuolelle kaksi nollaa. Kun nimittäin vähennetään kolmas rivi puolikkaalla kerrottuna toisesta rivistä ja kakkosella kerrottuna ensimmäisestä rivistä, saadaan matriisi
Tässä toisen rivin viimeisen luvun muuttaminen nollaksi vastaa sijoitusmenettelyyn perustuvassa ratkaisutavassa sitä, kun kolmannen muuttujan ratkaisu 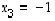 sijoitettiin yhtälöön (4) ja näin ratkaistiin muuttuja
sijoitettiin yhtälöön (4) ja näin ratkaistiin muuttuja 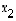 .
Ensimmäisen rivin viimeisen luvun muuttaminen nollaksi yhdessä seuraavan operaation kanssa vastaa sitä tilannetta, kun ratkaisujen
.
Ensimmäisen rivin viimeisen luvun muuttaminen nollaksi yhdessä seuraavan operaation kanssa vastaa sitä tilannetta, kun ratkaisujen 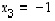 ja
ja 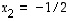 avulla ratkaistiin lopuksi muuttuja
avulla ratkaistiin lopuksi muuttuja 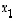 .
.
Kerroinmatriisissa saadaan toisen rivin avulla vielä yksi nolla ensimmäiselle riville, kun lisätään toinen rivi kolmella kerrottuna ensimmäiseen riviin:
Paluualgoritmikin on nyt valmis. Sen jälkeen kerroinmatriisissa pitäisi ihannetilanteessa olla lävistäjällä ykköset ja sekä sen ala- että yläpuolella nollat eli sen pitäisi olla ns. yksikkömatriisi.
Saadusta kaaviosta voidaan nyt suoraan lukea ratkaisu
sillä juuri tällaista yhtälöryhmäähän edellä oleva taulukko esittää, kun sen luvut sijoitetaan muuttujien kertoimiksi.
Yllä esitetty menettely on ns.
Gaussin ja Jordanin menetelmä lineaarisen yhtälöryhmän ratkaisemiseksi. Siinä pyritään siis yhtälöryhmän ratkaisemiseksi kaaviosta 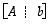 muotoa
muotoa 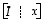 olevaan kaavioon, missä kerroinmatriisi
olevaan kaavioon, missä kerroinmatriisi 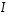 on yksikkömatriisi muodostuen siis ykkösistä lävistäjällä ja nollista muissa paikoissa. Tästä muodosta voidaan ratkaisu
on yksikkömatriisi muodostuen siis ykkösistä lävistäjällä ja nollista muissa paikoissa. Tästä muodosta voidaan ratkaisu 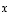 yksinkertaisesti lukea. Menetelmän suurin etu on siinä, että alkuperäisten yhtälöiden määrittelemät muuttujien väliset riippuvuudet kulkevat koko ajan täydellisenä tietoutena mukana ja lopuksi saatava ratkaisu on siten toimiva.
yksinkertaisesti lukea. Menetelmän suurin etu on siinä, että alkuperäisten yhtälöiden määrittelemät muuttujien väliset riippuvuudet kulkevat koko ajan täydellisenä tietoutena mukana ja lopuksi saatava ratkaisu on siten toimiva.
Gaussin ja Jordanin menetelmässä ovat seuraavat toimenpiteet sallittuja:
(1) Rivin kertominen nollasta eroavalla luvulla.
(3) Rivin monikerran lisääminen toiseen riviin.
Huomaa, että kaikki sallitut toimenpiteet koskevat vain rivejä. Sarakkeille tehtyinä vastaavat toimenpiteet eivät enää säilytä yhtälöryhmän yhtäpitävyyttä alkuperäisen kanssa (ne itse asiassa skaalaisivat muuttujia erilaisiksi tai vaihtaisivat niitä keskenään).
Menetelmässä sallittuja muokkauksia käsin tehtäessä voi käyttää esimerkiksi seuraavan taulukon mukaisia merkintöjä matriisin oikealla puolella. Painoteknisistä syistä näitä merkintöjä ei ole tässä kirjassa käytetty.
|
Kerrotaan nuolen alkupään osoittama rivi luvulla |
Kuten edellä varoiteltiin, Gaussin ja Jordanin menetelmä ei kuitenkaan aina mene yhtä säännöllisesti läpi kuin yllä eikä siten johda siihen ihanteelliseen muotoon, jossa muuttujien kertoimet muodostaisivat yksikkömatriisin. Toisaalta menetelmää voidaan käyttää myös silloin, kun muuttujia on eri määrä kuin yhtälöitä. Silloin menetelmässä pyritään muotoon, jossa neliömuotoinen yksikkömatriisi on vasemmassa yläkulmassa ja on kooltaan suurin taulukkoon mahtuva, jolloin sen ykkösrivi päättyy joko kerroinosan alalaitaan tai sen oikeaan reunaan.
Menetelmän käytössä voi vastaan tulla mm. seuraavanlaisia tilanteita, joissa on toimittava eri tavoin.
(a) Jos jossain vaiheessa tulee epätosi yhtälö 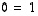 ,
esimerkiksi rivi
,
esimerkiksi rivi 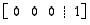 ,
yhtälöryhmällä ei ole ratkaisua. (Luvun 1 tilalla voi olla mikä tahansa nollasta eroava luku.)
,
yhtälöryhmällä ei ole ratkaisua. (Luvun 1 tilalla voi olla mikä tahansa nollasta eroava luku.)
(b) Jos taas vastaan tulee identtisesti tosi yhtälö 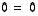 ,
esimerkiksi rivi
,
esimerkiksi rivi 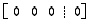 ,
tämä rivi ei rajoita ratkaisuja mitenkään ja yhtälöryhmällä voi silloin olla äärettömän monta ratkaisua. Jokainen sellainen muuttuja, jonka kaikki kertoimet tästä alaspäinkin ovat nollia, voidaan silloin valita ratkaisuun parametriksi. Ratkaisemista jatketaan seuraavalta riviltä normaaliin tapaan. Nollarivin voi myös siirtää alimmaksi riviksi.
,
tämä rivi ei rajoita ratkaisuja mitenkään ja yhtälöryhmällä voi silloin olla äärettömän monta ratkaisua. Jokainen sellainen muuttuja, jonka kaikki kertoimet tästä alaspäinkin ovat nollia, voidaan silloin valita ratkaisuun parametriksi. Ratkaisemista jatketaan seuraavalta riviltä normaaliin tapaan. Nollarivin voi myös siirtää alimmaksi riviksi.
(c) Jos yhtälöitä on enemmän kuin muuttujia, jolloin kerroinmatriisissa on rivejä enemmän kuin sarakkeita, ratkaisun olemassaoloa varten on 'ylijäämärivit' saatava identtisesti tosiksi eli esimerkiksi muotoon 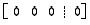 .
Jos sinne tulee yksikin epätosi yhtälö, yhtälöryhmällä ei ole ratkaisua.
.
Jos sinne tulee yksikin epätosi yhtälö, yhtälöryhmällä ei ole ratkaisua.
(d) Jos muuttujia on enemmän kuin yhtälöitä, jolloin kerroinmatriisissa on sarakkeita enemmän kuin rivejä, viimeisten sarakkeitten 'ylijääneet' muuttujat voidaan kukin valita omaksi parametrikseen ratkaisuun.
Muodostetaan sitä vastaava kaavio ja muokataan sitä:
Saatiin epätosi yhtälö 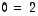 ,
joten yhtälöryhmällä ei ole ratkaisuja.
,
joten yhtälöryhmällä ei ole ratkaisuja.
Ratkaistaan sitten edellisestä hieman muutettu yhtälöryhmä
Muodostetaan taaskin sitä vastaava kaavio ja muokataan sitä:
Saatiin identtisesti tosi yhtälö 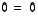 ,
joten toinen muuttuja
,
joten toinen muuttuja 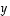 voidaan valita vapaasti. Ensimmäiseltä riviltä nähdään, että
voidaan valita vapaasti. Ensimmäiseltä riviltä nähdään, että 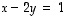 eli
eli 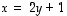 .
Parametrin avulla ilmoitettuna ratkaisu on siis
.
Parametrin avulla ilmoitettuna ratkaisu on siis
Muodostetaan ensin laajennettu kerroinmatriisi
ja muokataan sitä samoin säännöin kuin edellä. Vähennetään ensimmäinen rivi aluksi kahdella kerrottuna toisesta rivistä ja lisätään se sitten samalla kolmanteen riviin. Silloin saadaan kaavio
Nollaamalla toisen rivin avulla toisen sarakkeen alkiot ylä- ja alapuolelta (sekä muuttamalla toisen rivin lukujen merkit) saadaan kaavio
Kolmannen rivin avulla nollataan lopuksi kolmannen sarakkeen alkioita ja saadaan kaavio
Saatiin aikaan sten kaavio, jossa vasemmalla puolella on yksikkömatriisi. Tästä nähdään, että yhtälöryhmän ratkaisu on
Oletetaan seuraavissa tilanteissa, että yhtälöryhmään liittyvä laajennettu kerroinmatriisi on jo saatettu yksinkertaiseen muotoon. Keskitytäänkin kussakin tilanteessa siihen, miten lopullinen ratkaisu siitä päätellään. Kaikki tilanteet ovat jonkinlaisia erikoistapauksia. Ratkaistava vektorimuuttuja olkoon kaikissa tilanteissa komponenteista 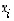 muodostuva vektori
muodostuva vektori 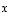 .
.
viimeinen rivi edustaa yhtälöä 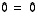 ,
joten se ei aiheuta rajoitteita ratkaisulle. Toiselta riviltä voidaan lukea, että
,
joten se ei aiheuta rajoitteita ratkaisulle. Toiselta riviltä voidaan lukea, että 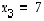 .
Ensimmäinen rivi taasen tarkoittaa yhtälöä
.
Ensimmäinen rivi taasen tarkoittaa yhtälöä 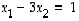 .
Koska muita rajoitteita ei ole, vain mainittu ehto sitoo kahta ensimmäistä muuttujaa toisiinsa nähden. Toinen niistä voidaan valita vapaasti ns. parametriksi (ja ratkaisuja on siten äärettömän paljon). Kun valitaan esimerkiksi, että
.
Koska muita rajoitteita ei ole, vain mainittu ehto sitoo kahta ensimmäistä muuttujaa toisiinsa nähden. Toinen niistä voidaan valita vapaasti ns. parametriksi (ja ratkaisuja on siten äärettömän paljon). Kun valitaan esimerkiksi, että 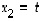 ,
saadaan koko yhtälöryhmän ratkaisuksi
,
saadaan koko yhtälöryhmän ratkaisuksi
Tämän ratkaisun hahmottaa ehkä vielä selvemmin, jos annetussa kerrointaulukossa viimeiset kaksi riviä vaihtaa ensin keskenään:
muuttujaa 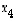 ei sido enää mikään ehto, joten se voidaan valita vapaaksi parametriksi. Muut ratkeavat yksikäsitteisesti. Ratkaisu on siten
ei sido enää mikään ehto, joten se voidaan valita vapaaksi parametriksi. Muut ratkeavat yksikäsitteisesti. Ratkaisu on siten
toinen yhtälö on muotoa 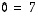 olevana mahdoton, joten kyseisellä yhtälöryhmällä ei ole ratkaisua ollenkaan.
olevana mahdoton, joten kyseisellä yhtälöryhmällä ei ole ratkaisua ollenkaan.
(a) graafisesti, (b) eliminointimenettelyllä ja (c) Gaussin ja Jordanin menetelmällä.