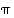Tehtävän 40 ratkaisu

Yksi tapa etsiä permutaation 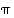käänteispermutaatio on kirjoittaa erillisten kiertojen tulo kaksirivisenä esityksenä, vaihtaa kaksirivisen esityksen rivit päikseen ja järjestää ylärivi kasvavaan järjestykseen.

Koska

niin

Käänteispermutaatio 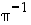saadaan selvitettyä myös seuraamalla läpi esiintyvät kierrot päinvastaisessa järjestyksessä. Ensinnäkin

,

joista saadaan siis kierto 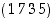. Samalla idealla löydetään käänteinen kierto (2 4 6), joten koko käänteispermutaatio esitettynä erillisten kiertojen tulona on .

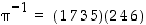Lisätietoja. Huomaa, että esim. kierrot (2 4 6), (6 2 4) ja (4 6 2) ovat vain eri esityksiä täsmälleen samalle kierrolle, jossa kakkonen kuvautuu neloseksi, nelonen kuutoseksi ja kuutonen kakkoseksi. Havaitaan, että näistä eri esityksistä (4 6 2) on permutaatiossa 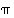esiintyneen kierron (2 6 4) "kierrätys" päinvastaisessa suunnassa. Käänteispermutaatio voidaankin muodostaa permutaation erillisten kiertojen esityksestä nopeasti vaihtamalla jokaisessa erillisessä kierrossa luvut vastakkaiseen järjestykseen.

Esimerkki. Yhden kierron tapauksessa esimerkiksi on .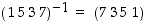

Esimerkki. Kahden erillisen kierron tulon käänteispermutaatio saadaan vastaavasti 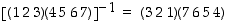. Huomaa kuitenkin, että tässä kiertojen erillisyys on olennaista. Jos kierrot eivät olisi erillisiä, olisi kertomisjärjestys myös vaihdettava. Erillisille kierroille kertomisjärjestyksellä ei kuitenkaan ole merkitystä.

[Opiskelutehtävä 40] [Vinkki tehtävään 40]

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]