[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
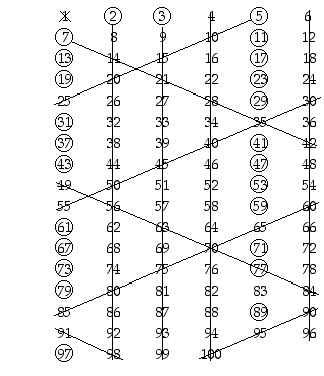
Käytetään hahmottamisapuna Eratostheneen seulaa (vrt. opiskelutehtävän 19 ratkaisu).
Seulasta näkyy, että 1. rivin jälkeen alkuluvut näyttävät löytyvän 1. ja 5. sarakkeelta. Toisaalta viimeinen sarake koostuu kuudella jaollisista luvuista, joten 1. sarakkeen luvut ovat näitä yhden isompia ja 5. sarakkeen luvut yhtä pienempiä. Ne ovat siten muotoa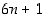 
ja 
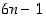. Perustellaan tämä tarkemmin.
Kun ei ole käytettävissä (eikä olemassa!) mitään sääntöä, josta kaikki alkuluvut voitaisiin muodostaa, ei sellaista väitettä, että alkuluvut olisivat tietyn muotoisia, voi suoraan todistaa. Täytyy siis käyttää epäsuoraa päättelyä. Kun nyt pitää osoittaa, että kaikki lukua 3 suuremmat alkuluvut ovat muotoa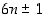 
jollekin 
,
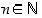on yhtäpitävää osoittaa, että mitkään muun muotoisista eivät ole alkulukuja. Tämä perustuu logiikan sääntöön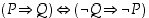 
,
missä nyt
P = "kokonaisluku
p on alkuluku,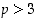 
" ja
Q = "
p on muotoa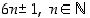 
".
Todistus tehdään seuraavasti: mikä tahansa kokonaisluku
p voidaan ilmoittaa jakoyhtälön avulla mm. muodossa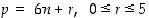 
. Vaihtoehtoisia tapauksia on siten kuusi kappaletta ja näistä 
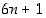ja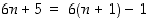 
ovat väitteen muotoisia. Muunlaisia kuin muotoa 
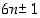olevia on siten neljänlaisia. Käydään niitten jaollisuus yksitellen läpi:
1° Kun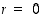 
,
niin 
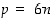on jaollinen luvulla 6.
2° Kun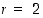 
,
niin 
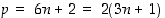on jaollinen luvulla 2.
3° Kun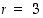 
,
niin 
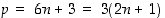on jaollinen luvulla 3.
4° Kun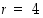 
,
niin 
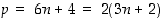on jaollinen luvulla 2.
Nämä ovat kaikki yhdistettyjä lukuja. Näin ollen voidakseen olla alkuluvun täytyy luvun
p olla muotoa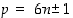 
.
Huomautus. Kaikki tätä muotoa olevat luvut eivät kuitenkaan ole alkulukuja. Esim. luvulle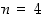 
on 
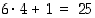jaollinen viitosella. Tässä siis havainnollistuu erittäin hyvin se, että implikaatiota ei saa automaattisesti "kääntää" tai lukea toisinpäin kuin se on kirjoitettu: nimittäin siitä, että
p on alkuluku, seuraa että se on yllä esitettyä muotoa, mutta siitä että luku on yllä esitettyä muotoa, ei välttämättä seuraa että se olisi alkuluku. Vaikka siis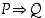 
pätee, ei välttämättä päde 
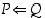eli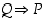 
.
Prime number research, records and resources: http://primes.utm.edu/
Patterns in primes: http://www.geocities.com/~harveyh/primes.htm
Prime number: http://en.wikipedia.org/wiki/Prime_number
Twin primes: http://mathworld.wolfram.com/TwinPrimes.html
The 1000 smallest primes: http://www.math.utah.edu/~pa/math/primelist.html
[Opiskelutehtävä 20] [Vinkki tehtävään 20]