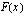 ääriarvot, kun
ääriarvot, kun 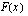 on funktion
on funktion 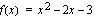 se integraalifunktio, jolle
se integraalifunktio, jolle 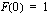 .
.
a ) Määritetään funktion 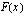 ääriarvot, kun
ääriarvot, kun 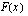 on funktion
on funktion 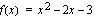 se integraalifunktio, jolle
se integraalifunktio, jolle 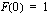 .
.
Lasketaan funktion 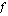 integraalifunktio
integraalifunktio 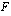 integroimalla termeittäin.
integroimalla termeittäin.
Määritetään vakio C siten, että ehto 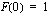 on voimassa.
on voimassa.
Annetun ehdon toteuttava funktion 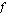 integraalifunktio
integraalifunktio 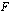 on:
on:
Funktion ääriarvot saadaan laskemalla funktion 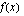 nollakohdat eli funktion
nollakohdat eli funktion 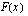 derivaatan nollakohdat eli mahdolliset ääriarvokohdat ja muodostamalla derivaatan merkkikaavio ääriarvojen luonteen tutkimiseksi.
derivaatan nollakohdat eli mahdolliset ääriarvokohdat ja muodostamalla derivaatan merkkikaavio ääriarvojen luonteen tutkimiseksi.
Nollakohdat saadaan toisen asteen yhtälön ratkaisukaavan avulla.
Muodostetaan derivaatan merkkikaavio.
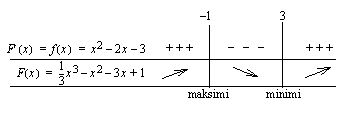
Funktiolla 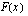 on lokaali maksimi kohdassa
on lokaali maksimi kohdassa 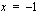 jolloin
jolloin
ja lokaali minimi kohdassa 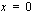 jolloin
jolloin
b ) Määritetään funktion 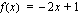 se integraalifunktio, jonka kuvaajan
se integraalifunktio, jonka kuvaajan 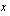 -akselista erottaman janan pituus on
-akselista erottaman janan pituus on 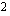 .
.
Lasketaan 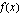 :n integraalifunktio
:n integraalifunktio 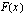 :
:
Integraalifunktio on toisen asteen polynomifunktio, jonka kuvaaja on paraabeli.
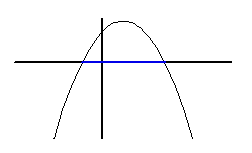
Seuraavaksi on määrättävä integroimisvakio 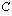 siten, että paraabelin ja
siten, että paraabelin ja 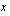 -akselin leikkauspisteiden määräämän janan pituus on 2. Lasketaan sitä varten integraalifunktion
-akselin leikkauspisteiden määräämän janan pituus on 2. Lasketaan sitä varten integraalifunktion 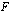 nollakohdat eli ratkaistaan yhtälö
nollakohdat eli ratkaistaan yhtälö 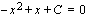 toisen asteen yhtälön ratkaisukaavan avulla:
toisen asteen yhtälön ratkaisukaavan avulla:
Ratkaistaan seuraavaksi integroimisvakio 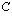 siten, että nollakohtien välinen etäisyys
siten, että nollakohtien välinen etäisyys 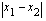 on
on 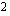 :
:
Koska neliöjuuri on aina suurempaa tai yhtäsuurta kuin nolla, voidaan itseisarvot jättää yhtälön ratkaisusta pois. Ratkaistaan 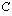 :
:
[Tehtävä 11.4][Vinkki tehtävään 11.4]