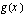 ja
ja 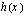 kuvaajien asymptootit, kun
kuvaajien asymptootit, kun
a ) Ratkaistaan funktioiden 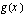 ja
ja 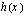 kuvaajien asymptootit, kun
kuvaajien asymptootit, kun
Rationaalifunktion 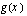 osoittajan asteluku on pienempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen -
osoittajan asteluku on pienempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen - 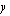 -akselin suuntainen suora - saadaan nimittäjän nollakohdasta
-akselin suuntainen suora - saadaan nimittäjän nollakohdasta 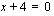 ja toinen on suora
ja toinen on suora 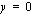 eli
eli 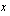 -akseli, sillä funktion raja-arvo, kun
-akseli, sillä funktion raja-arvo, kun 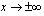 on nolla.
on nolla.
Funktion 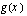 kuvaajalla on asymptootit
kuvaajalla on asymptootit 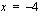 ja
ja 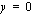 .
.
Rationaalifunktion 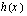 osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen -
osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptootit, joista toinen - 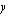 -akselin suuntainen suora - saadaan nimittäjän nollakohdasta
-akselin suuntainen suora - saadaan nimittäjän nollakohdasta 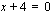 (sama kuin edellisellä funktiolla
(sama kuin edellisellä funktiolla 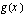 ) ja toinen - muotoa
) ja toinen - muotoa 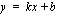 oleva suora - saadaan suorittamalla jakolasku
oleva suora - saadaan suorittamalla jakolasku 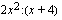 jakokulmassa ja jättämällä jäännöstermi huomiotta.
jakokulmassa ja jättämällä jäännöstermi huomiotta.
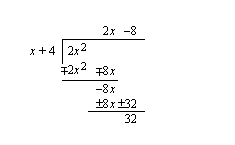
Funktion lauseke voidaan kirjoittaa muodossa:
Kun 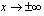 , niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa
, niin jäännöstermi lähestyy nollaa, jolloin funktion kuvaaja lähestyy suoraa 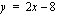 , mikä on funktion kuvaajan asymptootti.
, mikä on funktion kuvaajan asymptootti.
Funktion 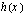 kuvaajalla on asymptootit
kuvaajalla on asymptootit 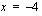 ja
ja 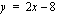 .
.
Kuvaajan piirtämistä varten määritetään funktion kuvaajan asymptootit. Rationaalifunktion 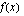 osoittajan asteluku on yhtäsuuri kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptoottina
osoittajan asteluku on yhtäsuuri kuin nimittäjän asteluku, joten funktion kuvaajalla on asymptoottina 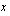 -akselin suuntainen suora
-akselin suuntainen suora 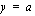 , missä
, missä 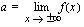 sekä
sekä 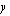 -akselin suuntaiset suorat, jotka saadaan nimittäjän nollakohdista
-akselin suuntaiset suorat, jotka saadaan nimittäjän nollakohdista 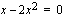 .
.
Funktion 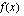 kuvaajalla on asymptootit
kuvaajalla on asymptootit 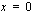 ,
, 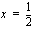 ja
ja 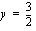 .
.
Funktion kuvaajan piirtämiseksi täytyy selvittää funktion vähenevyys/kasvavuus sekä ääriarvpisteet.
Funktion kuvaajan piirtämiseksi täytyy selvittää funktion vähenevyys/kasvavuus sekä ääriarvpisteet.
Ratkaistaan derivaatan nollakohdat eli funktion ääriarvokohdat toisen asteen yhtälön ratkaisukaavan avulla.
Muodostetaan derivaatan merkkikaavio funktion kasvavuuden/vähenevyyden tutkimiseksi ja ääriarvon laadun määrittämiseksi.
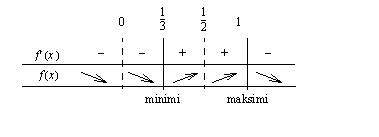
Funktio 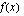 on aidosti kasvava, kun
on aidosti kasvava, kun 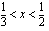 ja
ja 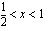 ja aidosti vähenevä, kun
ja aidosti vähenevä, kun 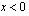 ,
, 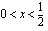 ja
ja 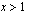 . Funktiolla on lokaali minimi kohdassa
. Funktiolla on lokaali minimi kohdassa 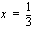 ja lokaali maksimi kohdassa
ja lokaali maksimi kohdassa 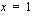 .
.
Rationaalifunktion kuvaaja voidaan nyt piirtää asymptoottien ja funktion käyttäytymisestä selvitettyjen tietojen avulla.
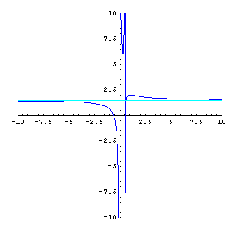
[Tehtävä 10.12][Vinkki tehtävään 10.12]