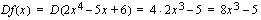
a ) Polynomifunktio voidaan derivoida termeittäin
b ) Tulon derivoimissäännön avulla
c ) Funktio on määritelty, kun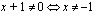 
. Osamäärän derivoimissäännön avulla
d ) Funktio on määritelty, kun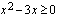 
eli tulon nollasäännön avulla ratkaistuna funktion 
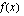ei ole määritelty, kun 
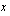kuuluu välille 
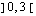. Ajatellaan funktio yhdistetyksi funktioksi, jossa ulkofunktio on 
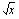ja sisäfunktio 
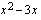. Yhdistetyn funktion derivoimissäännön avulla
e ) Osamäärän derivoimissäännön avulla
f ) Ajatellaan funktio funktion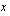 
ja yhdistetyn funktion 
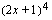tuloksi. Yhdistetyn funktion ulkofunktio on 
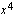ja sen derivaatta 
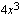sekä sisäfunktio 
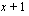ja sen derivaatta 
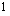. Tulon derivoimissäännön ja yhdistetyn funktion derivoimissäännön avulla
[Tehtävä 10.4][Vinkki tehtävään 10.4]
