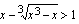on määritelty 
.
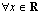Siirretään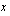 
epäyhtälön oikealle puolelle, jolloin sen etumerkki vaihtuu.
Korotetaan epäyhtälö puolittain kuutioon (Kolmanteen potenssiin korottaminen ei vaikuta yhtälön merkkeihin). Lasketaan binomin kuutio auki ja poistetaan sulut.
Yhtälön molemmilla puolilla on termi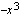 
, jotka kumoavat toisensa.
Siirretään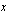 
epäyhtälön oikealle puolelle, jolloin sen etumerkki vaihtuu.
Epäyhtälö on saatu sievennettyä toisen asteen epäyhtälöksi, joka ratkaistaan laskemalla vastaavan yhtälön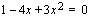 
juuret ja tekemällä merkkitarkastelu. Toisen asteen polynomifunktion 
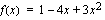kuvaaja on ylöspäin aukeava paraabeli, joten se saa negatiivisia arvoja nollakohtiensa välissä.
Juuret saadaan ratkaistua toisen asteen yhtälön ratkaisukaavalla
Alkuperäisen epäyhtälön ratkaisu on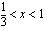 
b ) Epähtälö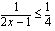 
on määritelty, kun 
.
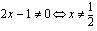Ratkaistaan murtoepäyhtälö siirtämällä kaikki termit epäyhtälön vasemmalle puolelle ja laventamalla ne samannimisiksi, jolloin ne voidaan laskea yhteen.
Epäyhtälön määrittelyssä on jo ratkaistu nimittäjän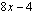 
nollakohta 
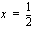ja osoittajan nollakohta saadaan yhtälöstä 
.
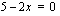Vähennetään yhtälön molemmilta puolilta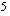 
ja jaetaan muuttujan 
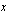kertoimella 
..
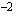Muodostetaan osamäärän merkkikaavio, jotta voidaan ratkaista epäyhtälö. Poistetaan ratkaisujoukosta mahdolliset nimittäjän nollakohdat.
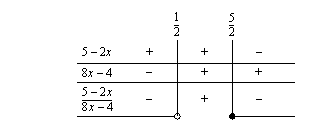
[Tehtävä 8.3][Vinkki tehtävään 8.3]
