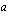 arvolla funktiolla
arvolla funktiolla 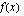 ei ole nollakohtia.
ei ole nollakohtia.
Ratkaistaan millä vakion 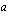 arvolla funktiolla
arvolla funktiolla 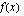 ei ole nollakohtia.
ei ole nollakohtia.
Ratkaistaan ensin funktion määrittelyjoukko ja etsitään sitten funktion vakiosta 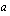 riippuvat nollakohdat ja määritetään
riippuvat nollakohdat ja määritetään 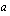 siten, että saadut ratkaisut eivät voi kuulua määrittelyjoukkoon.
siten, että saadut ratkaisut eivät voi kuulua määrittelyjoukkoon.
Murtofunktio ei ole määritelty nimittäjien 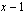 ja
ja 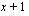 nollakohdissa
nollakohdissa 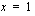 ja
ja 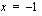 .
.
Ratkaistaan funktion nollakohdat ratkaisemalla yhtälö 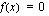 . Lavennetaan lausekkeet samannimisiksi ja lasketaan ne yhteen.
. Lavennetaan lausekkeet samannimisiksi ja lasketaan ne yhteen.
Käytetään tietoa, että osamäärä on nolla, kun osoittaja on nolla.
Vähennetään molemmilta puolilta yhtälöä 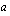 ja jaetaan muuttujan
ja jaetaan muuttujan 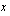 kertoimella
kertoimella 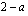 .
.
Funktiolla 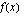 ei ole nollakohtia, kun
ei ole nollakohtia, kun
Saadaan ratkaistavaksi kaksi yhtälöä, jotka on määritelty, kun nimittäjä 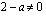 eli kun
eli kun 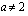 .
.
Kertomalla molemmat yhtälöt vasemman puolen nimittäjällä 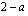 saadaan
saadaan
Lisätään ensimmäiseen yhtälöön molemmille puolille 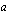 ja vähennetään toisen yhtälön molemmilta puolilta
ja vähennetään toisen yhtälön molemmilta puolilta 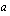 .
.
Ensimmäinen yhtälö on identtisesti epätosi ja toisen yhtälön ratkaisuksi saadaan jakamalla yhtälön molemmat puolet 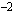 :lla
:lla 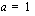
Funktiolla ei siis ole nollakohtia, kun vakio 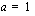 .
.
[Tehtävä 3.3][Vinkki tehtävään 3.3]