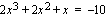.
Siirretään ensin kaikki termit yhtälön vasemmalle puolelle ja etsitään mahdollisten rationaalijuuri ehdokkaiden (vakiotermin tekijöiden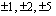 
suhde korkeimman asteen termin kertoimen tekijöihin 
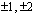) avulla yhtälön ratkaisua.
Rationaalijuuri ehdokkaat ovat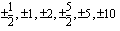 
.
Kokeillaan juurella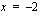 
: 
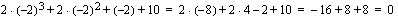, joka toteuttaa yhtälön. Kolmannen asteen polynomilla 
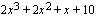on tekijä 
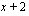. Ratkaistaan mahdolliset muut tekijät jakokulman avulla.
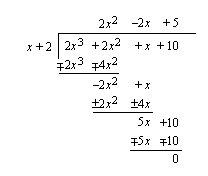
Polynomilla on tekijänä toisen asteen polynomi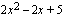 
, joten yhtälö 
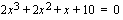voidaan nyt kirjoittaa yhtälön vasemman puolen polynomin tekijöiden avulla muodossa 
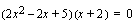. Tarkistetaan vielä onko toisen asteen tekijällä 
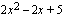juuria. Diskriminantin 
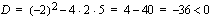perusteella tekijällä ei ole juuria.
Yhtälöllä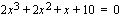 
on siis yksi ratkaisu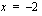 
[Tehtävä 2.4][Vinkki tehtävään 2.4]
