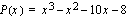 nollakohdat, kun tiedetään, että jaettaessa
nollakohdat, kun tiedetään, että jaettaessa 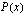 lausekkeella
lausekkeella 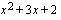 jako menee tasan.
jako menee tasan.
Ratkaise polynomifunktion 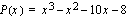 nollakohdat, kun tiedetään, että jaettaessa
nollakohdat, kun tiedetään, että jaettaessa 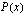 lausekkeella
lausekkeella 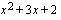 jako menee tasan.
jako menee tasan.
Tiedetään, että 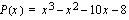 on jaollinen lausekkeella
on jaollinen lausekkeella 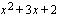 , joten jaetaan
, joten jaetaan 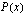 jakokulmassa tekijällään
jakokulmassa tekijällään 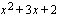 .
.
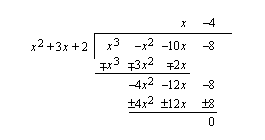
Polynomifunktion eräs tekijä on 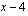 , joten sillä on nollakohta
, joten sillä on nollakohta 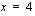 .
.
Tarkistetaan vielä onko toisen asteen tekijällä 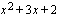 nollakohtia. Diskriminantin
nollakohtia. Diskriminantin 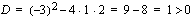 perusteella tekijällä on kaksi nollakohtaa, jotka saadaan toisen asteen yhtälön ratkaisukaavan avulla, kun ratkaistaan yhtälö
perusteella tekijällä on kaksi nollakohtaa, jotka saadaan toisen asteen yhtälön ratkaisukaavan avulla, kun ratkaistaan yhtälö 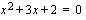 .
.
Kolmannen asteen polynomifunktion 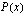 nollakohdat ovat:
nollakohdat ovat: 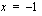 ,
, 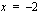 ja
ja 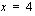 .
.
[Tehtävä 2.3][Vinkki tehtävään 2.3]