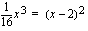.
Lasketaan ensin binomin neliö ja siirretään kaikki termit yhtälön vasemmalle puolelle (Etumerkit vaihtuvat). Kerrotaan yhtälö puolittain luvulla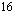 
, jotta saadaa kokonaislukukertoiminen yhtälö.
Etsitään mahdollisten rationaalijuuri ehdokkaiden (vakiotermin tekijöiden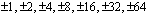 
suhde korkeimman asteen termin kertoimen tekijöihin 
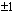) avulla yhtälön ratkaisua.
Rationaalijuuri ehdokkaat ovat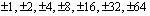 
.
Kokeilemalla huomataan, että juuri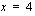 
käy: 
.
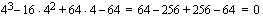Kolmannen asteen polynomilla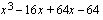 
on tekijä 
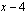. Ratkaistaan mahdolliset muut tekijät jakokulman avulla.
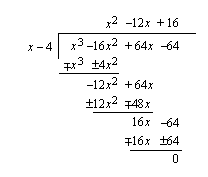
Polynomilla on tekijänä toisen asteen polynomi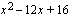 
, joten yhtälö 
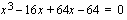voidaan nyt kirjoittaa yhtälön vasemman puolen polynomin tekijöiden avulla muodossa 
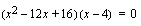. Tarkistetaan vielä onko toisen asteen tekijällä 
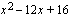juuria. Diskriminantin 
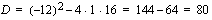perusteella tekijällä on kaksi juurta, jotka saadaan toisen asteen yhtälön ratkaisukaavan avulla, kun ratkaistaan yhtälö 
.
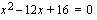Kolmannen asteen yhtälön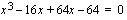 
juuret eli ratkaisut ovat: 
, 
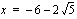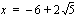ja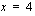 
.
[Tehtävä 2.5][Vinkki tehtävään 2.5]
.