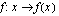Ratkaisu tehtävään 1.1

Funktio 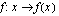on jatkuva ja aidosti vähenevä, joten kaikissa pisteissä on voimassa ehto

ja funktion arvojoukko on siten 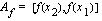, kun sen määrittelyjoukko on 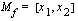. Lisäksi funktion 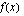aidosti vähenevyydestä seuraa, että funktiolla on käänteisfunktio 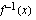, joka on jatkuva, sillä 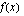on jatkuva.

a ) Edellisen perusteella jatkuvan ja aidosti vähenevän funktion, jonka määrittely joukko 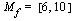, arvojoukko on .

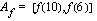b ) Edellisen perusteella funktion, jonka arvojoukko on 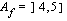, määrittelyjoukko on .

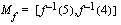[Tehtävä 1.1][Vinkki tehtävään 1.1]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]