HT 1.1.
Määrää jatkuvan ja aidosti vähenevän funktion 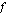 :
: 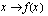
a ) arvojoukko 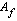 , kun määrittelyjoukko
, kun määrittelyjoukko 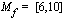 .
.
Määrää jatkuvan ja aidosti vähenevän funktion 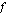 :
: 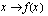
a ) arvojoukko 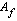 , kun määrittelyjoukko
, kun määrittelyjoukko 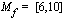 .
.
a ) Keksi ainakin kaksi erilaista funktioparia 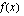 ja
ja 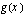 , jotka toteuttavat yhdistetyn funktion
, jotka toteuttavat yhdistetyn funktion
b ) Millainen sisäfunktio 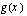 toteuttaa yhdistetyn funktion
toteuttaa yhdistetyn funktion 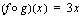 , kun ulkofunktio
, kun ulkofunktio
a ) Määritä 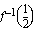 tuntematta käänteisfunktiota.
tuntematta käänteisfunktiota.
b ) Määritä 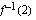 tuntematta käänteisfunktiota.
tuntematta käänteisfunktiota.
Mitä voit kertoa funktion nollakohdista, kun tiedetään, että funktion 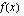 arvojoukko on
arvojoukko on 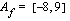 ja määrittelyjoukossaan
ja määrittelyjoukossaan 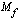 funktio on
funktio on
Toisen asteen polynomifunktiosta 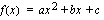 tiedetään. että sen
tiedetään. että sen
a ) Toisen asteen termin kerroin 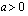 ja diskriminantti
ja diskriminantti 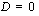 .
.
b ) Toisen asteen termin kerroin 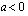 ja diskriminantti
ja diskriminantti 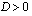 .
.
c ) Funktion nollakohdat ovat 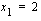 ja
ja 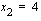 ja funktion kuvaaja on alaspäin aukeava paraabeli, jonka huippu sijaitsee
ja funktion kuvaaja on alaspäin aukeava paraabeli, jonka huippu sijaitsee 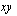 -koordinaatiston pisteessä (3, 4).
-koordinaatiston pisteessä (3, 4).
Piirrä kullekin tapaukselle esimerkkikuva. Määrää lisäksi funktio, joka toteuttaa ehdot.
Funktio 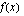 on parillinen jos
on parillinen jos 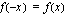 ja pariton jos
ja pariton jos 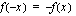 . Parillisen funktion kuvaaja on symmetrinen koordinaatiston y-akselin suhteen ja parittoman origon suhteen. Tutki ovatko seuraavat funktiot parillisia vai parittomia vai eivätkö kumpaakaan:
. Parillisen funktion kuvaaja on symmetrinen koordinaatiston y-akselin suhteen ja parittoman origon suhteen. Tutki ovatko seuraavat funktiot parillisia vai parittomia vai eivätkö kumpaakaan: