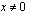Ratkaisu tehtävään 8.1

a ) Epäyhtälö on määritelty, kun .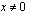

Tehtävässä voi edetä kahdella hieman eri tavalla.

Tapa 1

Lasketaan ensin jakolasku

siirretään sitten vakiotermi oikealle ja ratkaistaan yhtälö.

Tapa 2

Siirretään kaikki termit samalle puolelle ja lavennetaan ne samannimisiksi, jolloin ne voidaan laskea yhteen.

b ) Siirretään ensin kaikki termit epäyhtälön vasemmalle puolelle.

Epäyhtälön ratkaisemiseksi etsitään vastaavan yhtälön 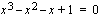juuret ja jaetaan polynomi tekijöihinsä. Mahdolliset rationaaliluku juuret saadaan kokonaislukukertoimiselle yhtälölle vakiotermin ja korkeimman asteen termin tekijöiden suhteena. Nyt ehdokkaita ovat 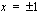, jotka molemmat toteuttavat yhtälön, joten ne ovat yhtälön juuria. Mahdollinen kolmas juuri saadaan jakamalla polynomi tekijällään 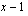jakokulman avulla (myös tekijällä 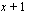jakamalla saadaan sama lopputulos).

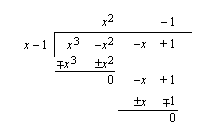
Polynomi voidaan nyt kirjoittaa tekijöidensä tulona summan ja erotuksen muistikaavaa apuna käyttäen.

Tehdään merkkikaavio, jonka avulla voidaan tutkia milloin epäyhtälö 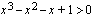on voimassa.

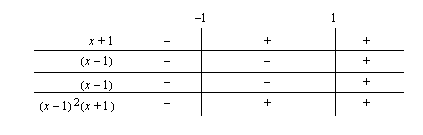
Epäyhtälö on siis voimassa, kun tulo 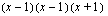on positiivinen eli kun .

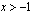[Tehtävä 8.1][Vinkki tehtävään 8.1]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]