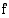 määritelty tietyllä välillä. Jos välin kaikissa pisteissä on voimassa ehto
määritelty tietyllä välillä. Jos välin kaikissa pisteissä on voimassa ehto
Olkoon funktio 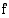 määritelty tietyllä välillä. Jos välin kaikissa pisteissä on voimassa ehto
määritelty tietyllä välillä. Jos välin kaikissa pisteissä on voimassa ehto
• 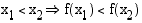 , funktio
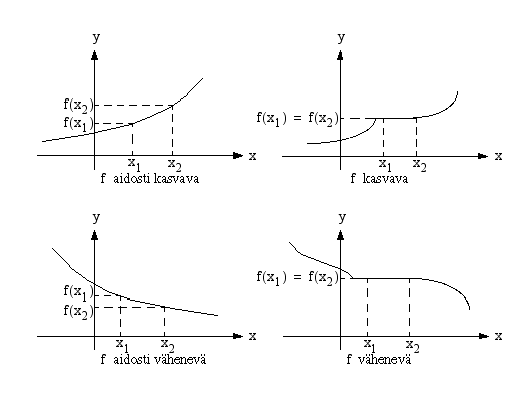
, funktio 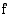 on aidosti kasvava.
on aidosti kasvava.
• 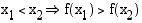 , funktio
, funktio 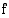 on aidosti vähenevä.
on aidosti vähenevä.
Jos funktio 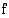 on koko välillä joko (aidosti) kasvava tai (aidosti) vähenevä, niin se on
(aidosti) monotoninen.
on koko välillä joko (aidosti) kasvava tai (aidosti) vähenevä, niin se on
(aidosti) monotoninen.
Jos funktio 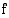 on aidosti monotoninen, se saa kunkin arvonsa vain kerran:
on aidosti monotoninen, se saa kunkin arvonsa vain kerran:
Aidosti kasvavan funktion 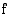 arvoilla
arvoilla 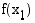 ja
ja 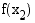 on sama suuruusjärjestys kuin vastaavilla muuttujan arvoilla
on sama suuruusjärjestys kuin vastaavilla muuttujan arvoilla 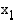 ja
ja 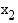 . Sanotaan, että aidosti kasvava funktio
. Sanotaan, että aidosti kasvava funktio 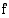 säilyttää järjestyksen, jolloin sille on voimassa
säilyttää järjestyksen, jolloin sille on voimassa
Aidosti vähenevän funktion 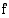 arvoilla
arvoilla 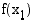 ja
ja 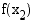 on puolestaan päinvastainen suuruusjärjestys kuin vastaavilla muuttujan arvoilla
on puolestaan päinvastainen suuruusjärjestys kuin vastaavilla muuttujan arvoilla 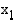 ja
ja 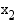 . Sanotaankin, että aidosti vähenevä funktio
. Sanotaankin, että aidosti vähenevä funktio 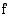 kääntää järjestyksen, jolloin sille on voimassa
kääntää järjestyksen, jolloin sille on voimassa
Monet yhtälöt ja epäyhtälöt voidaan ratkaista funktioiden monotonisuuteen perustuen.
Epäyhtälö on määritelty, kun juurrettavat ovat ei-negatiiviset eli 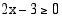 ja
ja 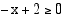 . Molemmat ehdot ovat voimassa, kun
. Molemmat ehdot ovat voimassa, kun 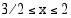 . Tiedetään, että neliöjuurifunktio on aidosti kasvava, sillä
. Tiedetään, että neliöjuurifunktio on aidosti kasvava, sillä
Koska aidosti kasvava funktio säilyttää järjestyksen, epäyhtälö 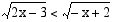 toteutuu, kun
toteutuu, kun 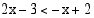 ja määrittelyehto on voimassa.
ja määrittelyehto on voimassa.
1. Olkoon funktio 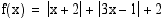 . Millä väleillä funktio
. Millä väleillä funktio 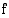 on
on
2. Tutki, millä reaaliluvun 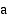 arvoilla funktio
arvoilla funktio 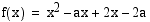 on aidosti kasvava, kun
on aidosti kasvava, kun 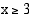 ?
?
3. Muodosta funktio 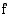 , jolla on seuraavat ominaisuudet:
, jolla on seuraavat ominaisuudet: 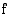 on aidosti kasvava, kun
on aidosti kasvava, kun 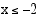 ja
ja 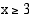 , ja
, ja 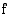 on aidosti vähenevä, kun
on aidosti vähenevä, kun 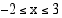 .
.
4. Keksi funktio 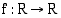 , joka ei ole kasvava eikä vähenevä millään reaalilukuvälillä.
, joka ei ole kasvava eikä vähenevä millään reaalilukuvälillä.