[edellinen] [sisällys] [seuraava]
3.3. Eksponentti- ja logaritmifunktio
Tässä luvussa esitellyille funktioille on runsaasti sovelluksia erilaisissa kasvumalleissa.
3.3.1. Eksponenttifunktio
Olemme jo harjoitelleet muodostamaan suureen kasvua kuvaavan funktion tapauksessa, jossa suureen määrä kasvaa tai vähenee aina yhtä monta prosenttia tietyssä aikayksikössä. Eräs tällainen tapaus on saldon kasvu kiinteäkorkoisella tilillä.
Esimerkki 3.8.
Talletetaan 2350 euroa tilille, jonka veroton korkokanta on 1,85 %/vuosi. Tilillä korko liitetään pääomaan aina vuoden kuluttua. Muodosta funktio, joka ilmoittaa tilin saldon 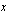 vuoden kuluttua talletushetkestä. Kuinka paljon tilillä olisi rahaa 8 vuoden kuluttua, jos tililtä ei tänä aikana nosteta varoja?
vuoden kuluttua talletushetkestä. Kuinka paljon tilillä olisi rahaa 8 vuoden kuluttua, jos tililtä ei tänä aikana nosteta varoja?
Seuraavasta taulukosta ilmenee, kuinka tilin saldo kasvaa vuosittain talletushetkestä alkaen.
Tilin saldon 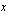 vuoden kuluttua talletushetkestä ilmoittaa funktio
vuoden kuluttua talletushetkestä ilmoittaa funktio
Päädyimme johdantoesimerkissämme funktioon, jossa muuttuja esiintyy eksponentissa. Tällaisia funktioita kutsutaan eksponenttifunktioiksi.
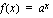 ,
,
missä kantaluku 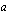 on jokin positiivinen vakio. Esimerkiksi
on jokin positiivinen vakio. Esimerkiksi 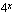 ja
ja 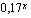 ovat eksponenttifunktioita. Koska kantaluvun ollessa positiivinen voi eksponentti olla mikä tahansa reaaliluku, on eksponentifunktio määritelty muuttujan
ovat eksponenttifunktioita. Koska kantaluvun ollessa positiivinen voi eksponentti olla mikä tahansa reaaliluku, on eksponentifunktio määritelty muuttujan 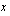 kaikilla reaaliarvoilla. Eksponenttifunktion kuvaaja riippuu tietysti kantaluvun arvosta. Oheisen oppimistehtävän avulla voit tutkia, miten kantaluvun arvo vaikuttaa eksponenttifunktion kuvaajaan.
kaikilla reaaliarvoilla. Eksponenttifunktion kuvaaja riippuu tietysti kantaluvun arvosta. Oheisen oppimistehtävän avulla voit tutkia, miten kantaluvun arvo vaikuttaa eksponenttifunktion kuvaajaan.
Oppimistehtävä 3.9.
http://www.cc.jyu.fi/~anvihola/testit/eksponentti.php
voit tutkia kantaluvun 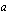 arvon vaikutusta eksponenttifunktion
arvon vaikutusta eksponenttifunktion 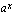 kuvaajaan. Voit antaa kantaluvulle
kuvaajaan. Voit antaa kantaluvulle 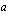 arvoja liikuttelemalla pistettä
arvoja liikuttelemalla pistettä 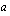 lukusuoralla. Tutki eksponenttifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin.
lukusuoralla. Tutki eksponenttifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin.
(a) Minkä pisteen kautta eksponenttifunktion kuvaaja aina kulkee? Miksi?
(b) Milloin funktio 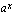 on aidosti kasvava?
on aidosti kasvava?
(c) Milloin funktio 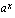 on vakio? Minka arvon funktio tuolloin saa kaikilla muuttujan arvoilla?
on vakio? Minka arvon funktio tuolloin saa kaikilla muuttujan arvoilla?
(d) Milloin funktio 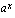 on aidosti vähenevä?
on aidosti vähenevä?
Taskulaskimissa on valmiina kaksi eri eksponenttifunktiota: 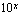 ja
ja 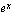 . Jälkimmäisen kantaluku on ns. Neperin luku
. Jälkimmäisen kantaluku on ns. Neperin luku 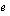 , joka on irrationaaliluku ja likiarvoltaan n. 2,71828. Kun näiden eksponenttifunktioiden arvo halutaan laskea tietyllä muuttujan
, joka on irrationaaliluku ja likiarvoltaan n. 2,71828. Kun näiden eksponenttifunktioiden arvo halutaan laskea tietyllä muuttujan 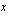 arvolla, näppäillään laskimeen ensin kyseinen muuttujan arvo ja painetaan sitten eksponenttifunktionäppäintä. Seuraavan testaa tietosi -tehtävän avulla voit varmistaa, että osaat laskea laskimellasi likiarvot mille tahansa eksponenttifunktion arvolle. Huomaa, että muiden eksponenttifunktioiden arvot saat laskettua potenssinäppäimen avulla.
arvolla, näppäillään laskimeen ensin kyseinen muuttujan arvo ja painetaan sitten eksponenttifunktionäppäintä. Seuraavan testaa tietosi -tehtävän avulla voit varmistaa, että osaat laskea laskimellasi likiarvot mille tahansa eksponenttifunktion arvolle. Huomaa, että muiden eksponenttifunktioiden arvot saat laskettua potenssinäppäimen avulla.
Testaa tietosi V
Laske kolmen desimaalin tarkkuudella
Lue nyt luentomonisteen luvusta 4.6.1, mitä siellä on kerrottu eksponenttifunktiosta. Katso erityisesti esimerkki 4.20 eksponenttiyhtälön ratkaisemisesta. Eksponenttifunktiolla voidaan kuvata kaikkia sellaisia kasvuilmiöitä, joissa suure esimerkiksi kolminkertaistuu tai kasvaa tietyn prosenttimäärän aina vakioajassa tai se vähenee esimerkiksi kolmasosan tai jonkun muun tietyn prosenttimäärän vakioajassa. Luentomonisteessa on esitetty joitakin esimerkkejä tällaisesta kasvamisesta tai vähenemisestä. Katso myös nuo esimerkit. Tällä kurssilla me pyrimme keskittymään sovelluksissa talous- ja arkielämän tilanteisiin.
Mainitessani edellä eksponenttiyhtälön tarkoitin yhtälöä, jossa tuntematon esiintyy eksponentissa. Tällaiset yhtälöt on tärkeää oppia ratkaisemaan, sillä niiden avulla voi määrittää ajan, jonka kuluttua suureen määrä on kasvanut tai vähentynyt tietylle tasolle. Monisteen esimerkistä 4.20 ilmenee yksi tapa eksponenttiyhtälön ratkaisemiseksi. Tätä tapaa voit käyttää silloin, kun yhtälön molemmat puolet voidaan esittää saman kantaluvun potensseina. Jos sinulla on ratkaistavana yhtälö
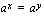 ,
,
voi se toteutua ainoastaan silloin, kun eksponentit ovat samat eli tässä 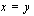 . Tiedämme, että kantaluvun ollessa positiivinen ja erisuuri kuin yksi, eksponenttifunktio on joko aidosti kasvava tai aidosti vähenevä. Tällainen funktio saa tietyn arvonsa vain kerran eli se ei voi saada samaa arvoa kahdessa eri pisteessä. Tämän nojalla arvot
. Tiedämme, että kantaluvun ollessa positiivinen ja erisuuri kuin yksi, eksponenttifunktio on joko aidosti kasvava tai aidosti vähenevä. Tällainen funktio saa tietyn arvonsa vain kerran eli se ei voi saada samaa arvoa kahdessa eri pisteessä. Tämän nojalla arvot 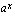 ja
ja 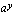 voivat olla yhtäsuuret ainoastaan, kun myös eksponentit ovat yhtäsuuret eli
voivat olla yhtäsuuret ainoastaan, kun myös eksponentit ovat yhtäsuuret eli 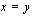 .
.
Kun olet muokannut eksponenttiyhtälön muotoon, jossa sen molemmilla puolilla on saman kantaluvun potenssit, ratkeaa yhtälö merkitsemällä noiden kantalukujen eksponentit yhtäsuuriksi. Mikäli eksponenttiyhtälössä ei voi kirjoittaa sen molempia puolia saman kantaluvun potensseina (se tavallisin tilanne), ratkaistaan yhtälö myöhemmin esitettävällä tavalla. Nyt voit kuitenkin harjoitella tätä ensin esiteltyä tapaa oheisen oppimistehtävän avulla.
Oppimistehtävä 3.10.
Toinen tapa eksponenttiyhtälön ratkaisemiseksi edellyttää meiltä aivan uuden käsitteen eli logaritmin tuntemista. Koska käytännön sovelluksiin liittyvissä tehtävissä juuri tuo toinen tapa on se, jonka avulla eksponenttiyhtälö yleensä ratkeaa, tarkastellaan näitä erilaisiin kasvuilmiöihin liittyviä sovelluksia vasta opiskeltuamme ensin logaritmin käsitteen.
3.3.2. Logaritmifunktio
Aloita opiskelusi lukemalla luentomonisteen luvusta 4.6.2 johdantoesimerkki 4.25. Esimerkin mukaan bakteeri jakautuu kerran tunnissa, joten 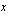 tunnin kuluttua bakteereja on jo
tunnin kuluttua bakteereja on jo 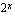 kpl. Nyt ollaan kiinnostuneita siitä, minkä ajan kuluttua bakteereja on tietty määrä. Mieti esimerkiksi, kuinka monen tunnin kuluttua bakteereja on jo 32, 256 tai 1024. Näitä bakteerimääriä vastaavat ajat saat ratkaistua kokeilemalla. Kutakin bakteerimäärää vastaa tietty aika, jonka kuluttua bakteerien määrä on kasvanut kyseisen suuruiseksi. Luentomonisteen johdantoesimerkissä oltiin kiinnostuneita siitä, minkä ajan kuluttua bakteereja on jo 7000. Tuo aika ratkaistiin esimerkissä likimääräisesti funktion
kpl. Nyt ollaan kiinnostuneita siitä, minkä ajan kuluttua bakteereja on tietty määrä. Mieti esimerkiksi, kuinka monen tunnin kuluttua bakteereja on jo 32, 256 tai 1024. Näitä bakteerimääriä vastaavat ajat saat ratkaistua kokeilemalla. Kutakin bakteerimäärää vastaa tietty aika, jonka kuluttua bakteerien määrä on kasvanut kyseisen suuruiseksi. Luentomonisteen johdantoesimerkissä oltiin kiinnostuneita siitä, minkä ajan kuluttua bakteereja on jo 7000. Tuo aika ratkaistiin esimerkissä likimääräisesti funktion 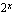 kuvaajan avulla. Vastaavaan tilanteeseen joudutaan aina, kun on selvitettävänä, minkä ajan kuluttua bakteerien määrä on kasvanut sellaiseksi, että kyseistä lukua ei osata kirjoittaa luvun 2 potenssina.
kuvaajan avulla. Vastaavaan tilanteeseen joudutaan aina, kun on selvitettävänä, minkä ajan kuluttua bakteerien määrä on kasvanut sellaiseksi, että kyseistä lukua ei osata kirjoittaa luvun 2 potenssina.
Ongelmamme on, kuinka ratkaistaan yhtälö
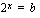 ,
,
olipa 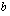 mikä tahansa positiivinen luku. Mietittävänä on siis se kantaluvun 2 eksponentti
mikä tahansa positiivinen luku. Mietittävänä on siis se kantaluvun 2 eksponentti 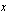 , joka antaa potenssin
, joka antaa potenssin 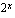 tuloksena luvun
tuloksena luvun 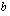 . Kyseistä eksponenttia kutsutaan luvun
. Kyseistä eksponenttia kutsutaan luvun 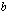 2-kantaiseksi logaritmiksi ja sitä merkitään
2-kantaiseksi logaritmiksi ja sitä merkitään 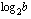 . Esimerkiksi
. Esimerkiksi
Määritellään nyt yleisesti luvun 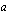 -kantainen logaritmi. Oletetaan, että kantaluku
-kantainen logaritmi. Oletetaan, että kantaluku 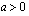 ja
ja 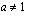 . Tällöin positiivisen luvun
. Tällöin positiivisen luvun 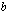
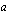 -kantainen logaritmi, jota merkitään
-kantainen logaritmi, jota merkitään
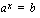 .
.
Positiivisen luvun 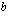
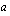 -kantainen logaritmi on siten se kantaluvun
-kantainen logaritmi on siten se kantaluvun 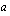 eksponentti
eksponentti 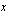 , joka antaa potenssin
, joka antaa potenssin 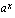 tulokseksi luvun
tulokseksi luvun 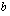 . Laskiessasi logaritmeja kysyt siis aina itseltäsi, mihin potenssiin kantaluku
. Laskiessasi logaritmeja kysyt siis aina itseltäsi, mihin potenssiin kantaluku 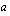 on korotettava, jotta saadaan luku
on korotettava, jotta saadaan luku 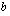 , jonka
, jonka 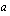 -kantaista logaritmia lasketaan.
-kantaista logaritmia lasketaan.
Huomaa, että logaritmi voidaan määrittää vain positiivisille luvuille, koska eksponenttifunktion arvot ovat aina positiivisia lukuja. Määrättäessä luvun 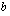
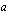 -kantaista logaritmia mietitään siis ratkaisua yhtälölle
-kantaista logaritmia mietitään siis ratkaisua yhtälölle 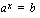 . Tällä yhtälöllä on ratkaisuja ainoastaan silloin, kun
. Tällä yhtälöllä on ratkaisuja ainoastaan silloin, kun 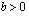 .
.
Lue nyt luentomonisteesta esimerkki 4.26, jossa on määrätty muutamia logaritmeja. Harjoittele sen jälkeen itse logaritmien laskemista oheisen oppimistehtävän avulla.
Oppimistehtävä 3.11.
Näin voit siis määrittää logaritmeja niissä tapauksissa, joissa pystyt ilmaisemaan luvun, jonka logaritmia olet laskemassa, kyseisen kantaluvun potenssina. Mikäli näin ei ole, voit kuitenkin määrittää logaritmin likiarvon laskimella. Taskulaskimissa on valmiina kaksi eri logaritmifunktiota: kymmenkantainen logaritmi ja 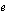 -kantainen logaritmi. Kymmenkantaista logaritmia kutsutaan Briggsin logaritmiksi ja sitä merkitään seuraavasti:
-kantainen logaritmi. Kymmenkantaista logaritmia kutsutaan Briggsin logaritmiksi ja sitä merkitään seuraavasti:
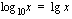 .
.
Neperin luku 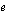 -kantaista logaritmia nimitetään puolestaan luonnolliseksi logaritmiksi, ja sitä merkitään
-kantaista logaritmia nimitetään puolestaan luonnolliseksi logaritmiksi, ja sitä merkitään
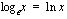 .
.
Laskimella näiden logaritmien arvot tietyille luvuille saadaan näppäilemällä ensin kyseinen luku ja painamalla sitten kyseisen logaritmifunktion näppäintä. Laskimella saadaan esimerkiksi kolmen desimaalin tarkkuudella seuraavat tulokset:
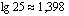 ja
ja 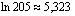 .
.
Kuinka sitten määrätään esimerkiksi 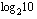 tai
tai 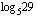 ? Niille saadaan laskimella likiarvo, kun ne on ensin ilmaistu 10-kantaisina tai luonnollisina logaritmeina. Logaritmeille voidaan johtaa laskusääntöjä, joita tarkastelemme myöhemmin hieman enemmään. Yksi tärkeimmistä logaritmien laskusäännöistä on ns. kannanvaihtokaava, jonka avulla logaritmi voidaan muuttaa toisen kantaluvun logaritmeiksi. Tästä kaavasta on hyötyä juuri logaritmien likiarvoja laskiessa, koska laskimella saa suoraan vain nuo kaksi logaritmia. Mikä tahansa logaritmi
? Niille saadaan laskimella likiarvo, kun ne on ensin ilmaistu 10-kantaisina tai luonnollisina logaritmeina. Logaritmeille voidaan johtaa laskusääntöjä, joita tarkastelemme myöhemmin hieman enemmään. Yksi tärkeimmistä logaritmien laskusäännöistä on ns. kannanvaihtokaava, jonka avulla logaritmi voidaan muuttaa toisen kantaluvun logaritmeiksi. Tästä kaavasta on hyötyä juuri logaritmien likiarvoja laskiessa, koska laskimella saa suoraan vain nuo kaksi logaritmia. Mikä tahansa logaritmi 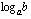 voidaan ilmaista
voidaan ilmaista 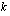 -kantaisina logaritmeina seuraavasti:
-kantaisina logaritmeina seuraavasti:
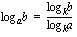 .
.
Kun logaritmi 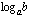 ilmaistaan
ilmaistaan 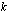 -kantaisten logaritmien avulla, tulee siitä kahden
-kantaisten logaritmien avulla, tulee siitä kahden 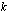 -kantaisen logaritmin osamäärä siten, että osoittajassa on luvun
-kantaisen logaritmin osamäärä siten, että osoittajassa on luvun 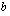
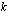 -kantainen logaritmi ja nimittäjässä kantaluvun
-kantainen logaritmi ja nimittäjässä kantaluvun 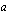
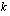 -kantainen logaritmi. Seuraava esimerkki näyttää, kuinka mille tahansa logaritmille saadaan laskimella likiarvo em. kannanvaihtokaavan avulla.
-kantainen logaritmi. Seuraava esimerkki näyttää, kuinka mille tahansa logaritmille saadaan laskimella likiarvo em. kannanvaihtokaavan avulla.
Esimerkki 3.12.
Oppimistehtävä 3.13.
Tarkastellaan sitten logaritmifunktiota 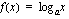 , missä kantaluku
, missä kantaluku 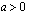 ja
ja 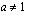 . Koska logaritmi voidaan määrittää vain positiivisille luvuille, on logaritmifunktio määritelty ainoastaan silloin, kun
. Koska logaritmi voidaan määrittää vain positiivisille luvuille, on logaritmifunktio määritelty ainoastaan silloin, kun 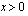 . Tämä sinun kannattaa muistaa aina logaritmeihin liittyviä tehtäviä - esimerkiksi yhtälöitä - ratkoessasi. Kuvaajan tarkastelu antaa havainnollisen kuvan funktion kulusta ja perusominaisuuksista. Sinun kannattaakin seuraavaksi paneutua oheiseen logaritmifunktion kuvaajaa tutkivaan oppimistehtävään.
. Tämä sinun kannattaa muistaa aina logaritmeihin liittyviä tehtäviä - esimerkiksi yhtälöitä - ratkoessasi. Kuvaajan tarkastelu antaa havainnollisen kuvan funktion kulusta ja perusominaisuuksista. Sinun kannattaakin seuraavaksi paneutua oheiseen logaritmifunktion kuvaajaa tutkivaan oppimistehtävään.
Oppimistehtävä 3.14.
http://www.cc.jyu.fi/~anvihola/testit/logaritmi.php
voit tutkia kantaluvun 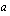 arvon vaikutusta logaritmifunktion
arvon vaikutusta logaritmifunktion 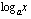 kuvaajaan. Voit antaa kantaluvulle
kuvaajaan. Voit antaa kantaluvulle 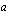 arvoja liikuttelemalla pistettä
arvoja liikuttelemalla pistettä 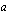 lukusuoralla. Tutki logaritmifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin.
lukusuoralla. Tutki logaritmifunktion käyttäytymistä ja vastaa sitten seuraaviin kysymyksiin.
(a) Minkä pisteen kautta logaritmifunktion kuvaaja aina kulkee? Miksi?
(b) Milloin funktio 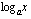 on aidosti kasvava?
on aidosti kasvava?
(c) Milloin funktio 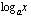 on aidosti vähenevä?
on aidosti vähenevä?
(d) Olkoon 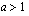 . Millä muuttujan
. Millä muuttujan 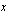 arvoilla logaritmifunktio
arvoilla logaritmifunktio 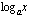 saa negatiivisia arvoja?
saa negatiivisia arvoja?
Harjoitellaan sitten ratkaisemaan yksinkertaisia yhtälöitä, joissa esiintyy logaritmeja. Tällaisia yhtälöitä ratkoessasi muista aina, että logaritmi on määritelty ainoastaan positiivisille luvuille. Kannattaa aina miettiä yhtälön määrittelyehto ennen ratkaisutoimenpiteiden aloittamista. Logaritmiyhtälöiden ratkaisemisesta on esimerkkejä luentomonisteessa. Katso sivulta 110 esimerkit 4.30 ja 4.31. Edellisessä sovelletaan logaritmin määritelmää, jonka mukaan
Oppimistehtävä 3.15.
Lopuksi tarkastelemme vielä paria sovellusesimerkkiä, joissa on määritettävä aika, jonka kuluttua eksponentiaalisesti kasvava suure on kasvanut tai vähentynyt tietylle tasolle. Kyseessä on eksponenttiyhtälön ratkaiseminen, jota jo edellä harjoittelimme eräissä erikoistapauksissa. Nyt esitettävä ratkaisutapa pätee yleisemmin ja on hyödyllinen opetella kaikkia niitä tilanteita varten, joissa on selvitettävä, minkä ajan kuluttua eksponentiaalinen kasvu on yltänyt tietylle tasolle.
Esimerkki 3.16.
Vuoden 2002 alussa talletetaan 3560 euroa tilille, jonka veroton korkokanta on 2 %/vuosi. Tilillä korko liitetään pääomaan aina vuoden lopussa. Milloin tilin saldo ylittää ensimmäisen kerran 4000 euroa, kun oletetaan, että tililtä ei nosteta eikä sinne lisätä varoja tänä aikana?
Oheisesta taulukosta ilmenee, kuinka tilin kokonaissaldo saadaan laskettua kunkin vuoden lopussa.
Kun selvitetään, milloin tilin saldo on 4000 euroa, on ratkaistava talletushetkestä kuluneiden vuosien määrä 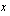 yhtälöstä
yhtälöstä
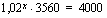 .
.
Muokataan yhtälö ensin muotoon, jossa muuttujan eksponentissaan sisältävä termi jää yksin yhtälön toiselle puolelle.
Tästä voidaan jälleen edetä kahdella eri ajattelutavalla. Yhtälön molemmat puolet ovat nyt positiiviset. Yhtälön molemmista puolista voidaan nyt ottaa samankantainen logaritmi (esim. luonnollinen logaritmi) yhtälön ratkaisujen muuttumatta.
Yhtälön vasemmalla puolella voidaan nyt soveltaa logaritmien laskusääntöä, jonka mukaan 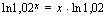 . Tämän jälkeen muuttuja ratkeaa samoin kuin tavallisessa ensimmäisen asteen yhtälössä. Huomaa, että yhtälön oikealla puolella on vain eräs reaaliluku, jonka likiarvo voidaan lopuksi laskea laskimella. Välivaiheissa käytämme luvusta tarkkaa arvoa.
. Tämän jälkeen muuttuja ratkeaa samoin kuin tavallisessa ensimmäisen asteen yhtälössä. Huomaa, että yhtälön oikealla puolella on vain eräs reaaliluku, jonka likiarvo voidaan lopuksi laskea laskimella. Välivaiheissa käytämme luvusta tarkkaa arvoa.
Tilin saldo ylittää siis 4000 euroa ensimmäisen kerran kuuden vuoden kuluttua eli vuoden 2007 lopussa.
Katsotaan vielä toinen tapa samaisen yhtälön ratkaisemiseksi. Kuten edellä päädytään yhtälöön
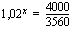 .
.
Logaritmin määritelmän mukaan se eksponentti 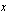 , johon korotettuna kantaluvun 1,02 potenssi
, johon korotettuna kantaluvun 1,02 potenssi 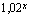 antaa tulokseksi luvun
antaa tulokseksi luvun 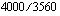 , on tämän luvun 1,02-kantainen logaritmi:
, on tämän luvun 1,02-kantainen logaritmi:
Huomaa, että molemmilla ajattelutavoilla päädyimme lopulta laskemaan likiarvoa aivan samalle luvulle.
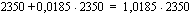
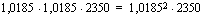
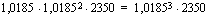


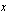
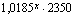
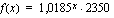 euroa.
euroa. 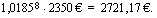
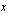 vuoden kuluttua talletushetkestä ilmoittaa funktio
vuoden kuluttua talletushetkestä ilmoittaa funktio 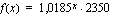 euroa.
euroa.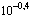 (b)
(b) 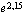 (c)
(c) 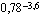
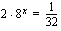 .
. 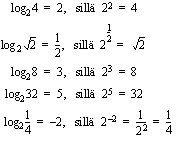
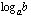 ,
,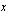 , joka toteuttaa yhtälön
, joka toteuttaa yhtälön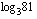 (b)
(b) 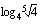 (c)
(c) 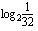 (d)
(d) 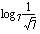 (e)
(e) 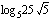
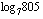 (b)
(b) 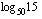
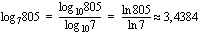
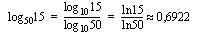
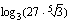 (b)
(b) 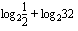 (c)
(c) 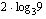
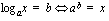 .
. 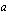 ollessa
ollessa 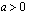 ja
ja 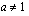 logaritmifunktio
logaritmifunktio 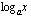 on joko aidosti kasvava tai aidosti vähenevä ja sellainen funktio saa tietyn arvonsa vain kerran. Logaritmifunktio ei siis voi saada samaa arvoa kahdessa eri pisteessä, vaan yhtälö
on joko aidosti kasvava tai aidosti vähenevä ja sellainen funktio saa tietyn arvonsa vain kerran. Logaritmifunktio ei siis voi saada samaa arvoa kahdessa eri pisteessä, vaan yhtälö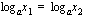
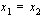 . Luettuasi em. esimerkit voit vielä harjoitella logaritmiyhtälöiden ratkaisemista oheisen oppimistehtävän avulla.
. Luettuasi em. esimerkit voit vielä harjoitella logaritmiyhtälöiden ratkaisemista oheisen oppimistehtävän avulla. 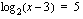 (b)
(b) 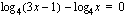
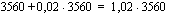
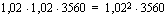
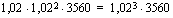


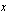
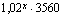
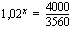
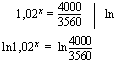
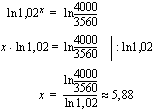
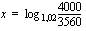 .
.