[edellinen] [sisällys] [seuraava]
2.5. Korkeamman asteen yhtälö ja epäyhtälö
Koska korkeamman asteen yhtälössä esiintyy aina vähintään kolmannen asteen polynomifunktio, on meidän syytä tarkastella aluksi polynomifunktioita yleisesti. Tähän mennessähän olemme tutustuneet niistä kahteen tavallisimpaan eli ensimmäisen ja toisen asteen polynomeihin.
2.5.1. Polynomifunktio
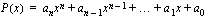 ,
,
missä 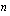 on jokin positiivinen kokonaisluku ja vakiot
on jokin positiivinen kokonaisluku ja vakiot 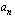 ,
, 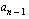 ,
,  ,
, 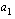 ja
ja 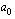 reaalilukuja siten, että
reaalilukuja siten, että 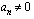 . Vakioiden alaindeksit ilmaisevat, minkä asteen termin kerroin on kyseessä. Polynomin korkeimman asteen potenssi
. Vakioiden alaindeksit ilmaisevat, minkä asteen termin kerroin on kyseessä. Polynomin korkeimman asteen potenssi 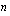 ilmoittaa polynomin asteluvun. Polynomifunktio on määritelty kaikilla reaaliluvuilla.
ilmoittaa polynomin asteluvun. Polynomifunktio on määritelty kaikilla reaaliluvuilla.
Esimerkiksi 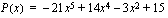 on viidennen asteen polynomifunktio, jonka viidennen asteen termin kerroin on -21, neljännen asteen termin kerroin on 14 jne. Polynomin kolmannen ja ensimmäisen asteen termien kertoimet ovat nollia. Polynomin
on viidennen asteen polynomifunktio, jonka viidennen asteen termin kerroin on -21, neljännen asteen termin kerroin on 14 jne. Polynomin kolmannen ja ensimmäisen asteen termien kertoimet ovat nollia. Polynomin  ns. vakiotermi on 15.
ns. vakiotermi on 15.
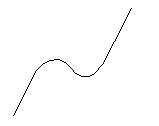
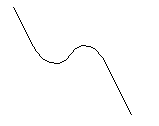
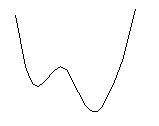
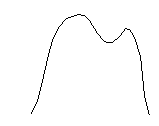
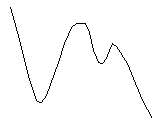
Polynomifunktion kuvaajan muoto riippuu polynomin asteluvusta sekä sen kertoimista. Tarkka kuvaaja määräytyy tapauskohtaisesti. Polynomin asteluvun  ja sen korkeimman asteen termin kertoimen
ja sen korkeimman asteen termin kertoimen  etumerkistä voidaan kuitenkin päätellä kuvaajan yleinen muoto vähän samaan tapaan kuin päättelimme toisen asteen polynomifunktion yhteydessä. Seuraava taulukko näyttää, kuinka polynomifunktion yleismuoto muuttuu asteluvun kasvaessa ja kuinka korkeimman asteen termin kerroin vaikuttaa siihen.
etumerkistä voidaan kuitenkin päätellä kuvaajan yleinen muoto vähän samaan tapaan kuin päättelimme toisen asteen polynomifunktion yhteydessä. Seuraava taulukko näyttää, kuinka polynomifunktion yleismuoto muuttuu asteluvun kasvaessa ja kuinka korkeimman asteen termin kerroin vaikuttaa siihen.
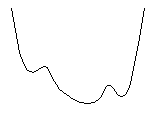
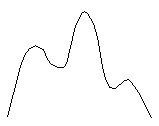
Polynomifunktion kuvaajalla ei suinkaan aina ole kaikkia oheisten kuvien kaltaisia huippukohtia. Kuvissa näkyy maksimimäärä näitä kohtia (eli paikallisia minimi- tai maksimikohtia), jotka kyseisen asteen polynomifunktiolla voi olla. Tietyn polynomifunktion kuvaaja on piirrettävä laskemalla siltä ensin riittävä määrä pisteitä. Myöhemmin modulissa 4, joka käsittelee differentiaalilaskentaa, opettelemme löytämään nuo funktion paikalliset minimi- ja maksimikohdat. Tämän jälkeen funktion kuvaaja on helppo piirtää niiden avulla, eikä meidän tarvitse laskea kuvaajalta kovin monta pistettä saadaksemme riittävän hyvän käsityksen funktion kulusta.
2.5.2. Korkeamman asteen yhtälö
Korkeamman asteen yhtälö voidaan aina sieventää muotoon
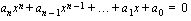 ,
,
missä vakiot 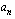 ,
, 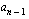 ,
,  ,
, 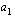 ja
ja 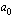 ovat reaalilukuja siten, että
ovat reaalilukuja siten, että 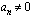 . Korkeamman asteen yhtälön ratkaiseminen merkitsee siten kyseisen polynomin nollakohtien etsimistä.
. Korkeamman asteen yhtälön ratkaiseminen merkitsee siten kyseisen polynomin nollakohtien etsimistä.
Korkeamman asteen yhtälön ratkaiseminen perustuu tulon nollasääntöön: kahden tai useamman tekijän tulo on nolla silloin ja vain silloin, kun jokin sen tekijöistä on nolla. Kun korkeamman asteen yhtälö on sievennetty perusmuotoon
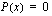 ,
,
missä 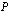 on vähintään kolmannen asteen polynomi, jaetaan polynomi
on vähintään kolmannen asteen polynomi, jaetaan polynomi 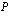 ensin tekijöihin eli esitetään se tulona, jonka tekijät ovat korkeintaan toista astetta. Tämän jäkeen yhtälö ratkeaa helposti tulon nollasäännöllä oheisen esimerkin osoittamalla tavalla.
ensin tekijöihin eli esitetään se tulona, jonka tekijät ovat korkeintaan toista astetta. Tämän jäkeen yhtälö ratkeaa helposti tulon nollasäännöllä oheisen esimerkin osoittamalla tavalla.
Esimerkki 2.19.
Edellisessä esimerkissä polynomin jakaminen tekijöihin oli helppoa, koska löysimme kaikista termeistä yhteisen tekijän. Seuraavaksi onkin syytä pohtia, kuinka tämä onnistuu silloin, kun emme löydä yhteistä tekijää. Polynomin tekijöihin jakaminen on korkeamman asteen yhtälöiden ratkaisemisen vaikein vaihe. Jokainen polynomi voidaan jakaa ensimmäistä tai toista astetta oleviin tekijöihin nollakohtiensa avulla. Tätä tietoa hyödynnämme nyt korkeamman asteen yhtälöiden ratkaisussa.
Esimerkki 2.20.
Edellisen esimerkin nojalla tiedetään, että polynomin 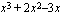 nollakohtia ovat
nollakohtia ovat 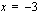 ,
, 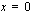 ja
ja 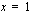 . Tämä merkitsee sitä, että polynomi on jaollinen
. Tämä merkitsee sitä, että polynomi on jaollinen 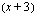 :lla,
:lla, 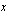 :llä ja
:llä ja 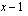 :llä. Laske
:llä. Laske
(a) Suoritetaan jakolasku jakokulmassa oheisen kuvion osoittamalla tavalla.
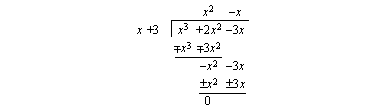
(b) Toinen kohta menee samalla tavalla kuin edellinen. Voit harjoitella polynomin jakolaskua jakokulmassa itse tämän (b)-kohdan avulla.
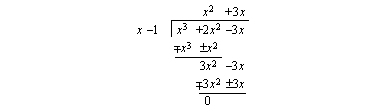
Aina, kun 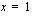 on polynomin nollakohta, tämä polynomi on jaollinen
on polynomin nollakohta, tämä polynomi on jaollinen 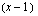 :llä eli jakolasku päättyy tasan. Mikäli saat laskiessasi jakojäännöksen, olet joko tehnyt virheen jakolaskussa tai vastaava luku ei olekaan polynomin nollakohta.
:llä eli jakolasku päättyy tasan. Mikäli saat laskiessasi jakojäännöksen, olet joko tehnyt virheen jakolaskussa tai vastaava luku ei olekaan polynomin nollakohta.
Jos polynomilla 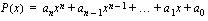 on
on  nollakohtaa
nollakohtaa  , niin jokaista nollakohtaa
, niin jokaista nollakohtaa  vastaa tekijä
vastaa tekijä 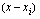 ja polynomi
ja polynomi 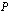 voidaan esittää tulona
voidaan esittää tulona
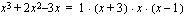 .
.
Polynomilla 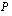 , jonka asteluku on
, jonka asteluku on 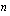 , on enintään
, on enintään 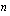 reaalista nollakohtaa, joten
reaalista nollakohtaa, joten 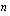 :nnen asteen yhtälöllä
:nnen asteen yhtälöllä 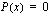 on korkeintaan
on korkeintaan 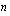 reaalijuurta.
reaalijuurta.
Korkeamman asteen yhtälön ratkaiseminen edellyttää siis yhden ratkaisun löytämistä jollakin muulla tavalla. Tämä ensimmäinen nollakohta löydetään yleensä arvaamalla tai kokeilemalla. Tätä toivottomalta kuulostavaa arvaamista ja kokeilua helpottaa seuraava tieto:
on rationaalinen ratkaisu 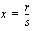 , niin tuon ratkaisun osoittaja
, niin tuon ratkaisun osoittaja 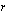 on polynomin
on polynomin 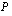 vakiotermin
vakiotermin 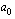 tekijä ja nimittäjä
tekijä ja nimittäjä 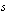 on sen korkeimman asteen termin kertoimen
on sen korkeimman asteen termin kertoimen 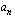 tekijä. Jos on ratkaistavana esimerkiksi yhtälö
tekijä. Jos on ratkaistavana esimerkiksi yhtälö
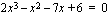 ,
,
on vastaavan polynomin vakiotermi 6 eli yhtälön rationaalijuuren osoittaja on jokin tämän luvun tekijöistä, joita ovat 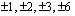 . Rationaalijuuren nimittäjä on puolestaan jokin korkeimman asteen termin kertoimen tekijä. Tuo kerroin on nyt 2, joten nimittäjä on
. Rationaalijuuren nimittäjä on puolestaan jokin korkeimman asteen termin kertoimen tekijä. Tuo kerroin on nyt 2, joten nimittäjä on 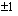 tai
tai 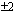 . Mahdolliset rationaalijuuret ovat nyt
. Mahdolliset rationaalijuuret ovat nyt
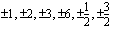 .
.
Jos näistä kokeilemalla löytyy yhtälölle yksi ratkaisu, löytyvät muut juuret jakamalla polynomi kyseistä nollakohtaa vastaavalla tekijällä ja käyttämällä tulon nollasääntöä, kun polynomi on ensin jaettu tekijöihin. Mikäli yksikään rationaalijuurivaihtoehto ei toteuta yhtälöä, ovat yhtälön ratkaisut irrationaalisia tai niitä ei ole lainkaan. Tällaisessa tapauksessa on tyydyttävä likimääräiseen ratkaisuun, joka löydetään esimerkiksi kuvaajan perusteella tai jollakin numeerisella menetelmällä sopivaa laskulaitetta apuna käyttäen.
Lue nyt luentomonisteen luvusta 2.4.1, mitä siellä on kerrottu korkeamman asteen yhtälön ratkaisemisesta. Katso erityisesti esimerkit 2.15 ja 2.16. Edellisestä näet, kuinka korkeamman asteen yhtälö ratkeaa tässä esitetyllä periaatteella. Jälkimmäinen esimerkki on erikoistapauksesta, jossa voi hyödyntää toisen asteen yhtälön ratkaisukaavaa eikä edellisen kaltaista tekijöihin jakamista tarvita lainkaan. Opiskeltuasi nuo esimerkit on sinun vuorosi kokeilla korkeamman asteen yhtälön ratkaisemista oheisten oppimistehtävien avulla.
2.5.3. Korkeamman asteen epäyhtälö
Korkeamman asteen epäyhtälö voidaan aina sieventää muotoon
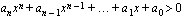 ,
,
missä suurempi kuin -merkin tilalla voi tietenkin olla mikä tahansa muu epäyhtälömerkki. Korkeamman asteen epäyhtälöä ratkaistaessa etsitään siis niitä muuttujan arvoja, joilla vastaava polynomi 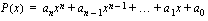 saa esim. positiivisia arvoja.
saa esim. positiivisia arvoja.
Korkeamman asteen epäyhtälön ratkaisu perustuu tulon merkkisääntöön: tulo on negatiivinen täsmälleen silloin, kun pariton määrä sen tekijöistä on negatiivisia. Epäyhtälön ratkaisijan on ensin jaettava vastaava polynomi tekijöihin samoin kuin vastaavaa yhtälöä ratkaistaessa tehtäisiin. Tämän jälkeen on selvitettävä kustakin korkeintaan toista astetta olevasta tekijästä sen nollakohdat ja etumerkki eri väleillä. Tekijän etumerkin päättely onnistuu kätevästi esimerkiksi sen kuvaajan avulla samalla tavoin kuin tehtiin toisen asteen epäyhtälöitä ratkaistaessa. Korkeamman asteen epäyhtälön ratkaiseminen onnistuu kätevimmin merkkikaavion avulla. Merkkikaavioon varataan oma rivi kutakin polynomin tekijää kohden sekä yksi rivi, jonne niiden tulon etumerkki voidaan päätellä. Merkkikaavioon piirretään pystyviiva kutakin polynomin nollakohtaa varten. Nuo nollakohdat merkitään pystyviivoille suuruusjärjestyksessä. Kunkin pystyviivan välissä polynomin tietty tekijä saa joko vain positiivisia tai vain negatiivisia arvoja. Kutakin tekijää vastaavalle riville on ensin merkittävä + ja - merkit sen mukaan, saako tekijä kyseisellä välillä positiivisia vai negatiivisia arvoja. Tämän jälkeen päätellään niiden tuloa vastaavalle riville tulon etumerkki tulon nollasäännön avulla. Kun polynomin tekijöiden tulon etumerkki tiedetään eri väleillä, osataan myös vastata varsinaiseen kysymykseen sen mukaan, etsittiinkö epäyhtälössä niitä muuttujan arvoja, joilla polynomi saa positiivisia vai negatiivisia arvoja.
Lue nyt luentomonisteesta korkeamman asteen epäyhtälöitä käsittelevä luku 2.4.2 ja katso huolella sen esimerkki 2.17. Tämän esimerkin merkkikaaviota laadittaessa polynomin tekijöiden merkit eri väleillä on päätelty seuraavien kuvaajien avulla:
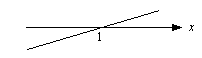 Tekijän
Tekijän 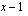 kuvaaja on nouseva suora, joten se saa negatiivisia arvoja nollakohtansa
kuvaaja on nouseva suora, joten se saa negatiivisia arvoja nollakohtansa 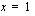 vasemmalla puolella ja positiivisia arvoja tämän nollakohdan oikealla puolella.
vasemmalla puolella ja positiivisia arvoja tämän nollakohdan oikealla puolella. 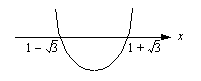 Tekijän
Tekijän 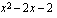 kuvaaja on ylöspäin aukeava paraabeli, joten tämä tekijä saa negatiivisia arvoja nollakohtiensa
kuvaaja on ylöspäin aukeava paraabeli, joten tämä tekijä saa negatiivisia arvoja nollakohtiensa 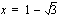 ja
ja 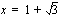 välissä ja positiivisia arvoja niiden ulkopuolella.
välissä ja positiivisia arvoja niiden ulkopuolella. Kun korkeamman asteen epäyhtälöä ratkaistaessa vastaava polynomi on jaettu korkeintaan toista astetta oleviin tekijöihin, ovat eri tekijöiden kuvaajat aina joko suoria tai paraabeleja. Päätelläksesi tekijän etumerkin eri väleillä sinun on siis ensin selvitettävä sen nollakohdat. Tämän jälkeen voit päätellä etumerkin eri väleillä tekijän kuvaajan avulla samoin kuin edellä tehtiin. Kuvaajasta sinun on vain tiedettävä, onko se nouseva vai laskeva suora tai ylöpäin vai alaspäin aukeava paraabeli.
Kokeile vielä korkeamman asteen epäyhtälön ratkaisemista seuraavan oppimistehtävän avulla. Siinä esiintyvä funktio on sama kuin oppimistehtävässä 2.21, joten voit keskittyä opettelemaan sitä, mikä on olennaista korkeamman asteen epäyhtälön ratkaisemisessa eli merkkikaavion laadintaa.
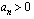
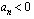
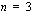
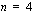

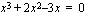 .
.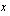 yhteiseksi tekijäksi. Käytetään sitten tulon nollasääntöä.
yhteiseksi tekijäksi. Käytetään sitten tulon nollasääntöä. 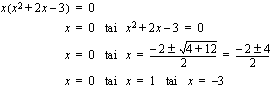
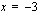 ,
, 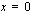 tai
tai 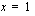
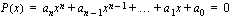 ,
,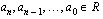 ja
ja 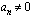 . Jos luku
. Jos luku 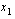 on polynomin
on polynomin 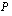 nollakohta ts.
nollakohta ts. 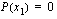 , niin
, niin 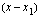 on polynomin
on polynomin 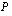 yksi tekijä. Tämä tarkoittaa sitä, että polynomi
yksi tekijä. Tämä tarkoittaa sitä, että polynomi 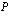 voidaan tällöin esittää tulona, jonka toinen tekijä on
voidaan tällöin esittää tulona, jonka toinen tekijä on 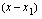 ja toinen jokin
ja toinen jokin 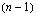 :nnen asteen polynomi:
:nnen asteen polynomi: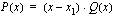 .
.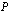 tekijäpolynomi, jota edellä on merkitty
tekijäpolynomi, jota edellä on merkitty 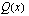 :llä, löydetään jakamalla polynomi
:llä, löydetään jakamalla polynomi 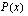 tekijällä
tekijällä 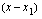 jakokulmassa seuraavassa esimerkissä opetettavalla tavalla. Kun polynomin
jakokulmassa seuraavassa esimerkissä opetettavalla tavalla. Kun polynomin 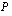 asteluku on
asteluku on 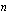 , on sen
, on sen 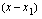 :llä jakamisen avulla löydetyn toisen tekijäpolynomin
:llä jakamisen avulla löydetyn toisen tekijäpolynomin 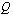 asteluku on
asteluku on 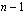 .
. 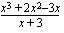 (b)
(b) 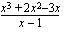
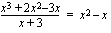 (b)
(b) 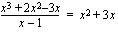
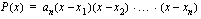 .
. 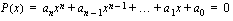
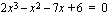 .
. 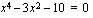 .
. 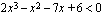 .
.