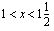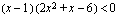,
jossa epäyhtälön polynomi on jaettu korkeintaan toista astetta oleviin tekijöihin. Samaisen oppimistehtävän perusteella tiedämme, että tekijän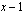 
nollakohta on 
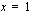ja tekijän 
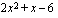nollakohdat 
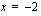ja 
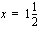. Laaditaan nyt merkkikaavio, josta ilmenee näiden tekijöiden sekä niiden tulon merkki eri väleillä. Koska tekijän 
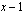kuvaaja on nouseva suora, joka leikkaa 
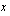-akselin kohdassa 
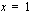, saa tämä tekijä positiivisia arvoja nollakohtansa oikealla ja negatiivisia arvoja sen vasemmalla puolella. Koska toisen tekijän 
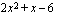kuvaaja on ylöspäin aukeava paraabeli, saa tämä tekijä positiivisia arvoja nollakohtiensa 
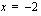ja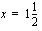 
ulkopuolella ja negatiivisia arvoja niiden välissä. Tulon merkkisäännöllä voidaan päätellä näiden tekijöiden tulon etumerkki eri väleillä.
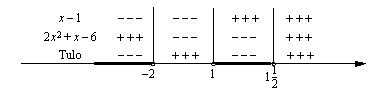
Merkkikaavion perusteella polynomi, joka voidaan esittää kaaviossa esitettyjen tekijöiden tulona, saa negatiivisia arvoja, kun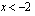 
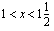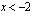tai 
.
tai 