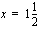Kuten aiemmin jo todettiin, polynomin vakiotermi on 6 eli yhtälön rationaalijuuren osoittaja on jokin tämän luvun tekijöistä 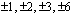 . Rationaalijuuren nimittäjä on puolestaan jokin korkeimman asteen termin kertoimen 2 tekijöistä
. Rationaalijuuren nimittäjä on puolestaan jokin korkeimman asteen termin kertoimen 2 tekijöistä 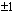 tai
tai 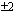 . Mahdolliset rationaalijuuret ovat nyt
. Mahdolliset rationaalijuuret ovat nyt
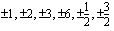 .
.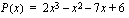 .
. 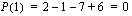 , joten
, joten 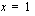 on polynomin nollakohta ja polynomi on jaollinen
on polynomin nollakohta ja polynomi on jaollinen 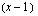 :llä. Jaetaan polynomi tällä tekijällä.
:llä. Jaetaan polynomi tällä tekijällä. 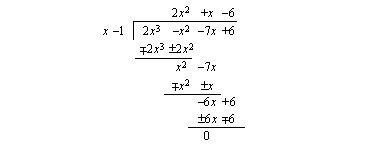
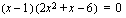 .
.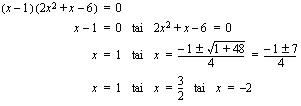
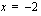 ,
, 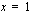 tai
tai