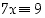 renkaassa
renkaassa 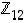 . Koska
. Koska 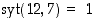 ,
on alkio 7 kääntyvä tässä renkaassa (ks. lause 3.4.1) ja näin ollen yhtälölle on olemassa yksikäsitteinen ratkaisu.
,
on alkio 7 kääntyvä tässä renkaassa (ks. lause 3.4.1) ja näin ollen yhtälölle on olemassa yksikäsitteinen ratkaisu.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Ratkaistavana on yhtälö 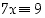 renkaassa
renkaassa 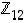 . Koska
. Koska 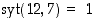 ,
on alkio 7 kääntyvä tässä renkaassa (ks. lause 3.4.1) ja näin ollen yhtälölle on olemassa yksikäsitteinen ratkaisu.
,
on alkio 7 kääntyvä tässä renkaassa (ks. lause 3.4.1) ja näin ollen yhtälölle on olemassa yksikäsitteinen ratkaisu.
Lauseen 3.4.4 nojalla ratkaisu on muotoa 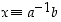 ,
missä
,
missä 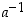 on alkion
on alkion 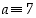 käänteisalkio ja
käänteisalkio ja 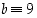 . Siten täytyy ensin etsiä alkion 7 käänteisalkio. Edellisen opiskelutehtävän 31 ratkaisun mukaan sen käänteisalkio on se itse. Tämän näkee myös siitä, sillä
. Siten täytyy ensin etsiä alkion 7 käänteisalkio. Edellisen opiskelutehtävän 31 ratkaisun mukaan sen käänteisalkio on se itse. Tämän näkee myös siitä, sillä 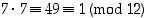 . Nyt alkio
x voidaan ratkaista:
. Nyt alkio
x voidaan ratkaista:
Lisätietoja. Huomaa, että ratkaisu on nimenomaan koko se ekvivalensiluokka, jonka yksi edustaja on alkio 3. Yleensä renkaassa 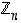 ekvivalenssiluokan edustajaksi valitaan se luokan (yksikäsitteinen) jäsen
a,
jolle
ekvivalenssiluokan edustajaksi valitaan se luokan (yksikäsitteinen) jäsen
a,
jolle 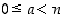 . Voitaisiin kuitenkin valita mikä tahansa kyseisen luokan (tässä tapauksessa luokan
. Voitaisiin kuitenkin valita mikä tahansa kyseisen luokan (tässä tapauksessa luokan 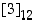 ) edustaja muuttujaksi
x ja edelleen pyydetty yhtälö toteutuisi.
) edustaja muuttujaksi
x ja edelleen pyydetty yhtälö toteutuisi.
Esimerkki. Koska 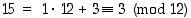 ,
voidaan valita
,
voidaan valita 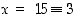 ,
jolloin
,
jolloin 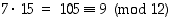 ,
sillä
,
sillä 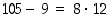 . Edelleen voitaisiin valita ekvivalenssiluokan edustajaksi
. Edelleen voitaisiin valita ekvivalenssiluokan edustajaksi 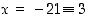 ,
jolloin
,
jolloin 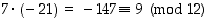 ,
sillä
,
sillä 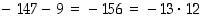 .
.
[Opiskelutehtävä 32] [Vinkki tehtävään 32]